A magnet is taken towards a conducting ring in such a way that a constant current of 10mA is induced in it. The total resistance of the ring is 0.5Ω. In 5s, the magnetic flux through the ring changes by
0.25mWb
25mWb
50mWb
15mWb
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Identify the given quantities
- Induced current I=10mA=10×10−3A
- Resistance of the ring R=0.5Ω
- Time duration Δt=5s
Step 2: Use the relationship between charge, current, and time
The charge ΔQ induced can be calculated using the formula:
ΔQ=I×Δt
Substituting the values:
ΔQ=(10×10−3A)×(5s)=50×10−3C=0.05C
Step 3: Relate charge to change in magnetic flux
The change in magnetic flux ΔΦ can be expressed in terms of the charge and resistance using the formula:
ΔQ=ΔΦR
Rearranging this gives:
ΔΦ=ΔQ×R
Step 4: Substitute the values to find the change in magnetic flux
Now substituting the values of ΔQ and R:
ΔΦ=(0.05C)×(0.5Ω)=0.025Wb
Step 5: Convert to milliWebers
To express the result in milliWebers:
ΔΦ=0.025Wb=25mWb
Final Answer
The change in magnetic flux through the ring is ΔΦ=25mWb.
---
- Induced current I=10mA=10×10−3A
- Resistance of the ring R=0.5Ω
- Time duration Δt=5s
The charge ΔQ induced can be calculated using the formula:
ΔQ=I×Δt
Substituting the values:
ΔQ=(10×10−3A)×(5s)=50×10−3C=0.05C
The change in magnetic flux ΔΦ can be expressed in terms of the charge and resistance using the formula:
ΔQ=ΔΦR
Rearranging this gives:
ΔΦ=ΔQ×R
Now substituting the values of ΔQ and R:
ΔΦ=(0.05C)×(0.5Ω)=0.025Wb
To express the result in milliWebers:
ΔΦ=0.025Wb=25mWb
The change in magnetic flux through the ring is ΔΦ=25mWb.
Topper's Solved these Questions
Similar Questions
The resistance of a coil is 5 ohm and a current of 0.2A is induced in it due to a varying magnetic field. The rate of change of magnetic flux in it will be-
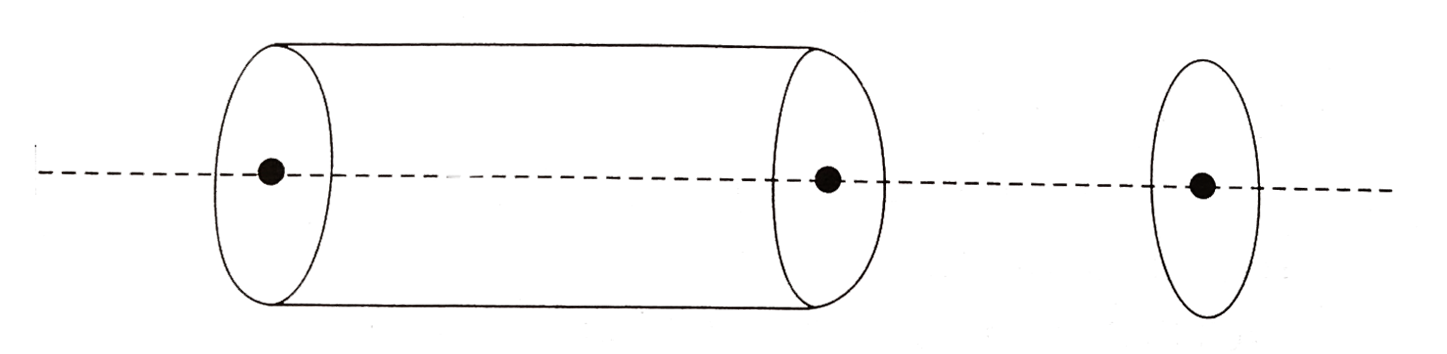
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View Solution
Knowledge Check
By a change of current from 5 A to 10 A in 0.1 s, the self induced emf is 10 V. The change in the energy of the magnetic field of a coil will be
A5JB6JC7.5JD9JBy a change of current from 5 A to 10 A in 0.1 s, the self induced emf is 10 V. The change in the energy of the magnetic field of a coil will be
A5JB6JC7.5JD9J
The diagram shows a solenoid carrying time varying current I=I0t (I0 is constant) on the axis of this solenoid a conducting ring is being placed as shown in the figure. The mutual inductance of the ring and the solenoid is M and self inductance of the ring is L . if the resistance of the ring is R then the maximum current which can flow through the ring is
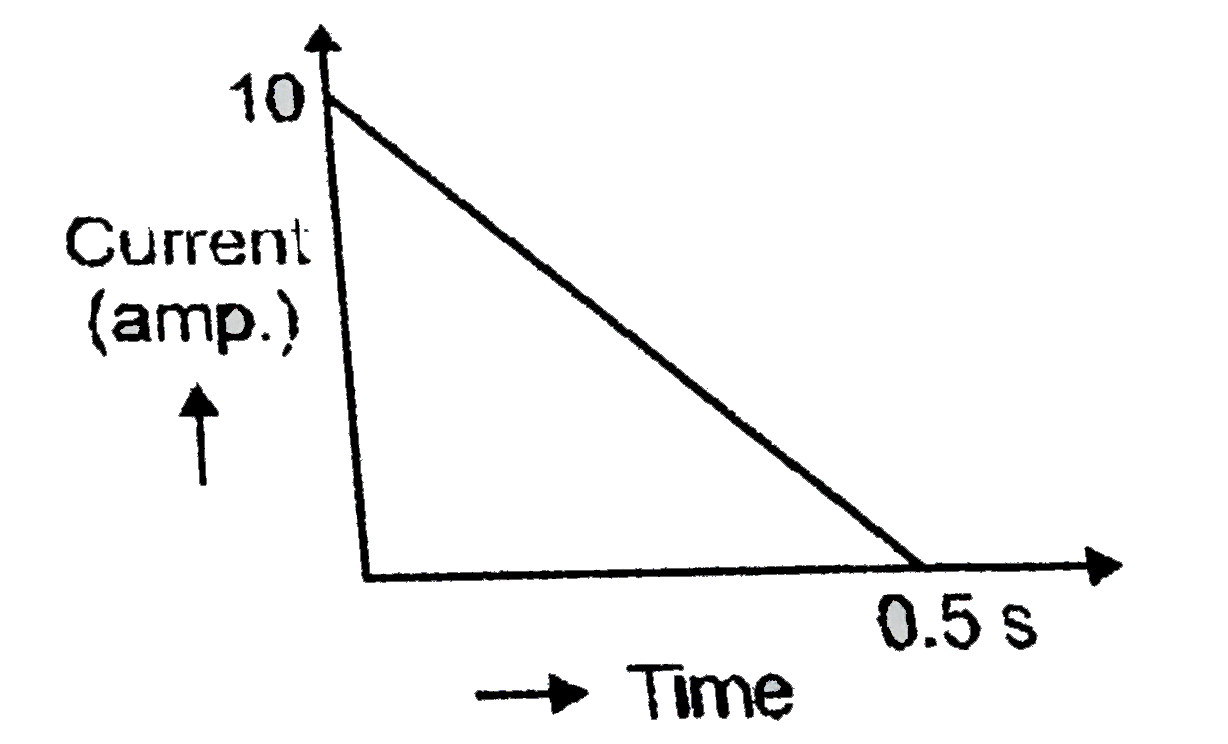
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
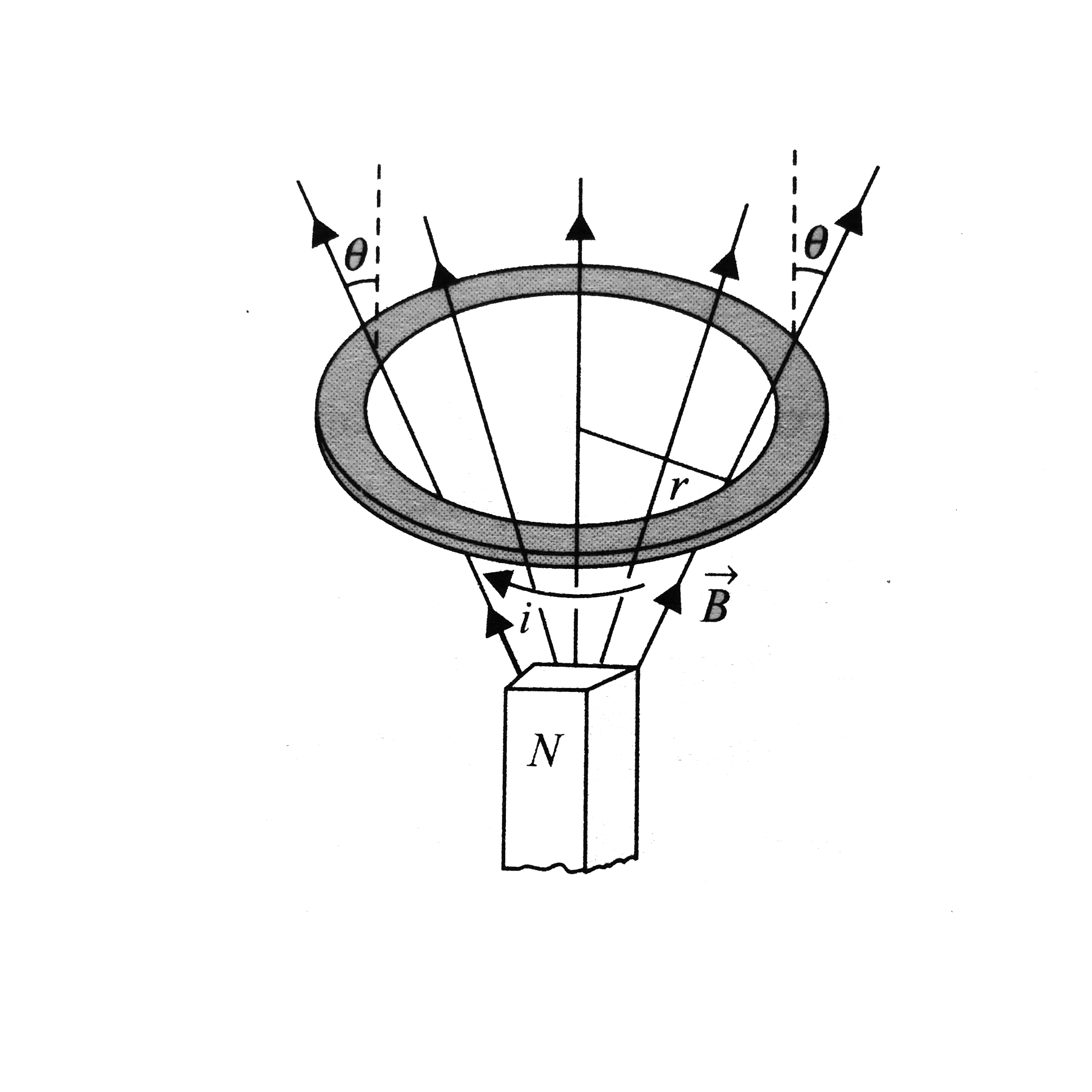
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
View SolutionMagnetic flux of 5 microweber is linked with a coil, when a current of 1mA flows through it. What is the self-inductance of the coil?
View SolutionA thin circular ring of area A is held perpendicular to a uniform magnetic field of induction B. A small cut is made in the ring and a galvanometer is connected across the ends such that the total resistance of the circuit is R. When the ring is suddenly squeezed to zero area, the charge flowing through the galvanometer is
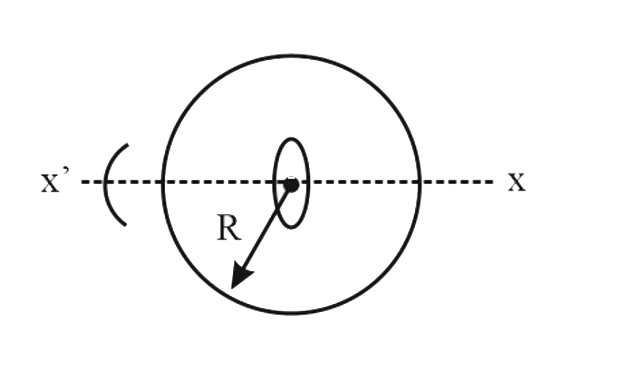
View SolutionA non-conducting ring of radius R having uniformly distributed charge Q starts rotating about x-x' axis passing through diameter with an angular acceleration α, as shown in the figure. Another small conducting ring having radius a(a<<R) is kept fixed at the centre of bigger ring is such a way that axis xx' is passing through its centre and perpendicular to its plane. If the resistance of small ring is r=1Ω , find the induced current in it in ampere.
(Given q=16×102μ0C,R=1m,a=0.1m,α=8rad s−2
View Solution
