A metal disc of radius a rotates with a constant angular velocity ω about its axis. The potential difference between the center and the rim of the disc is (m = mass of electron, e = charge on electro)
mω2a2e
12mω2a2e
mω2a22m
mω2a2m
The correct Answer is:A
To find the potential difference between the center and the rim of a rotating metal disc, we can follow these steps:
Step 1: Understand the System
We have a metal disc of radius a rotating with a constant angular velocity ω. We need to find the potential difference between the center of the disc and a point on its rim.
Step 2: Identify Forces Acting on an Electron
An electron at a distance r from the center of the disc experiences a centripetal force due to its circular motion. This centripetal force is provided by the electric force acting on the electron due to the electric field E generated by the rotation of the disc.
Step 3: Write the Expression for Centripetal Force
The centripetal force Fc acting on the electron can be expressed as:
Fc=mω2r
where m is the mass of the electron, ω is the angular velocity, and r is the distance from the center.
Step 4: Relate Electric Force to Centripetal Force
The electric force Fe acting on the electron is given by:
Fe=eE
where e is the charge of the electron and E is the electric field at distance r. Since the electric force provides the centripetal force, we have:
eE=mω2r
Step 5: Find the Electric Field
From the above equation, we can express the electric field E as:
E=mω2re
Step 6: Calculate the Potential Difference
The small potential difference dV when moving a small distance dr is given by:
dV=Edr
Substituting the expression for E:
dV=mω2redr
Step 7: Integrate to Find Total Potential Difference
To find the total potential difference V between the center (where r=0) and the rim (where r=a), we integrate:
V=∫a0mω2redr
Calculating the integral:
V=mω2e∫a0rdr=mω2e(r22)a0=mω2e⋅a22
Thus, the potential difference V is:
V=mω2a22e
Final Answer
The potential difference between the center and the rim of the disc is:
V=mω2a22e
---
We have a metal disc of radius a rotating with a constant angular velocity ω. We need to find the potential difference between the center of the disc and a point on its rim.
An electron at a distance r from the center of the disc experiences a centripetal force due to its circular motion. This centripetal force is provided by the electric force acting on the electron due to the electric field E generated by the rotation of the disc.
The centripetal force Fc acting on the electron can be expressed as:
Fc=mω2r
where m is the mass of the electron, ω is the angular velocity, and r is the distance from the center.
The electric force Fe acting on the electron is given by:
Fe=eE
where e is the charge of the electron and E is the electric field at distance r. Since the electric force provides the centripetal force, we have:
eE=mω2r
From the above equation, we can express the electric field E as:
E=mω2re
The small potential difference dV when moving a small distance dr is given by:
dV=Edr
Substituting the expression for E:
dV=mω2redr
To find the total potential difference V between the center (where r=0) and the rim (where r=a), we integrate:
V=∫a0mω2redr
Calculating the integral:
V=mω2e∫a0rdr=mω2e(r22)a0=mω2e⋅a22
Thus, the potential difference V is:
V=mω2a22e
The potential difference between the center and the rim of the disc is:
V=mω2a22e
Similar Questions
A metal disc of radius R=25cm rotates with a constant angular velocity ω=130 rad s−1 about its axis. Find the potential difference between the center and rim of the disc if
(a) the external magnetic field is absent,
(b) the external uniform magnetic field B=5.0mT directed perpendicular to the disc.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA metal disc of radius R rotates with an angular velcoity ω about an axis perpendiclar to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View SolutionA uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1nqωr2. Find the value of n.
View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
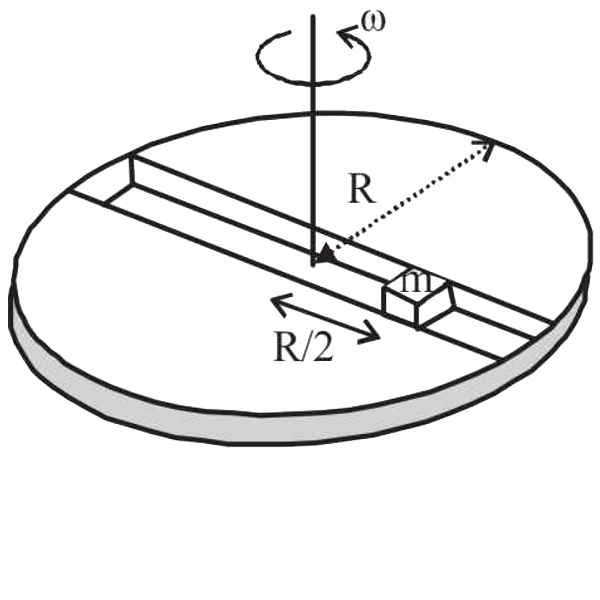
The net reaction of the disc on the block is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
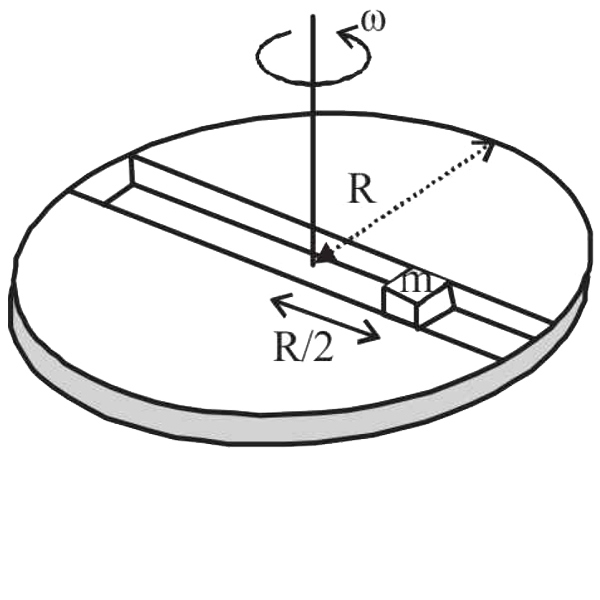
The distance r of the block at time is
View Solution
