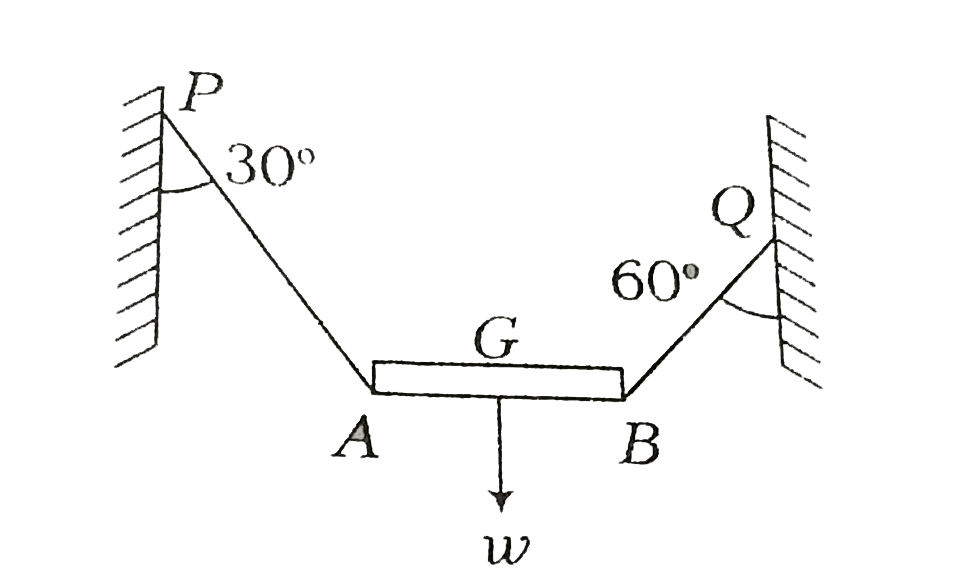
A non-uniform rod AB of weight w is supported horizontally in a vertical plane by two light strings PA and QB as shown in the figure.G is the centre of gravity of the rod. If PA and QB make angles 30∘ and 60∘ respectively with the vertical, the ratio AGGB is
12
√3
13
1√3
The correct Answer is:C
( c) T1cos60∘=T2sin60∘⇒T12=√3T22

or T1cos60∘=T2sin60∘
or T1=√3T2…….(i)
√3T12×AG=T22×BG
∴AGBG=T2√3T1
But T2T1=1√3 [ from Eq. (i)]
Hence, AGBG=13
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
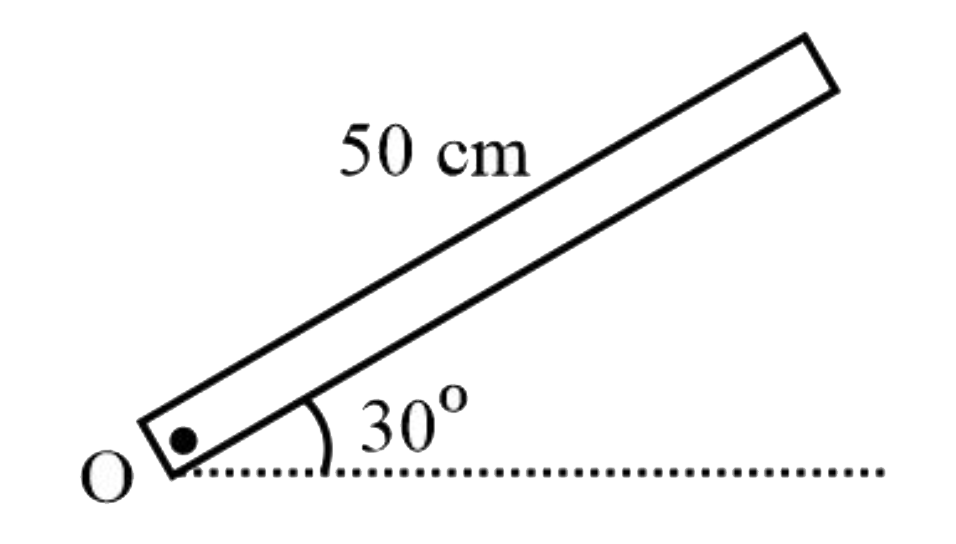
A uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View Solution
Knowledge Check
A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
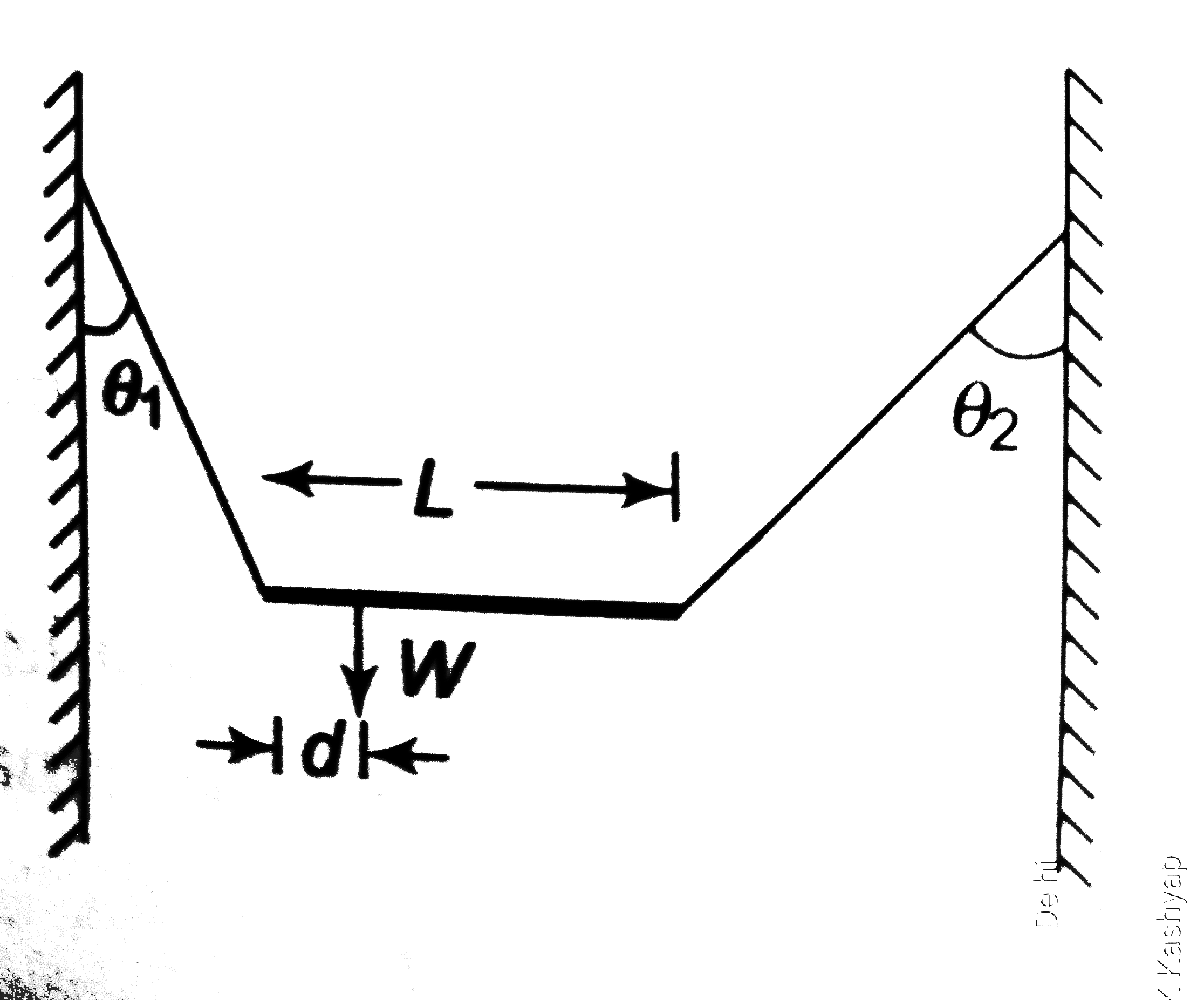 .AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
.AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)

A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of weight Fg and length L is supported at its ends by a frictionless through as shown in figure. (a) Show that the centre of gravity of the rod must be vertically over point O when the rod is in equilibrium. (b) Determine the equilibrium value of the angle θ.

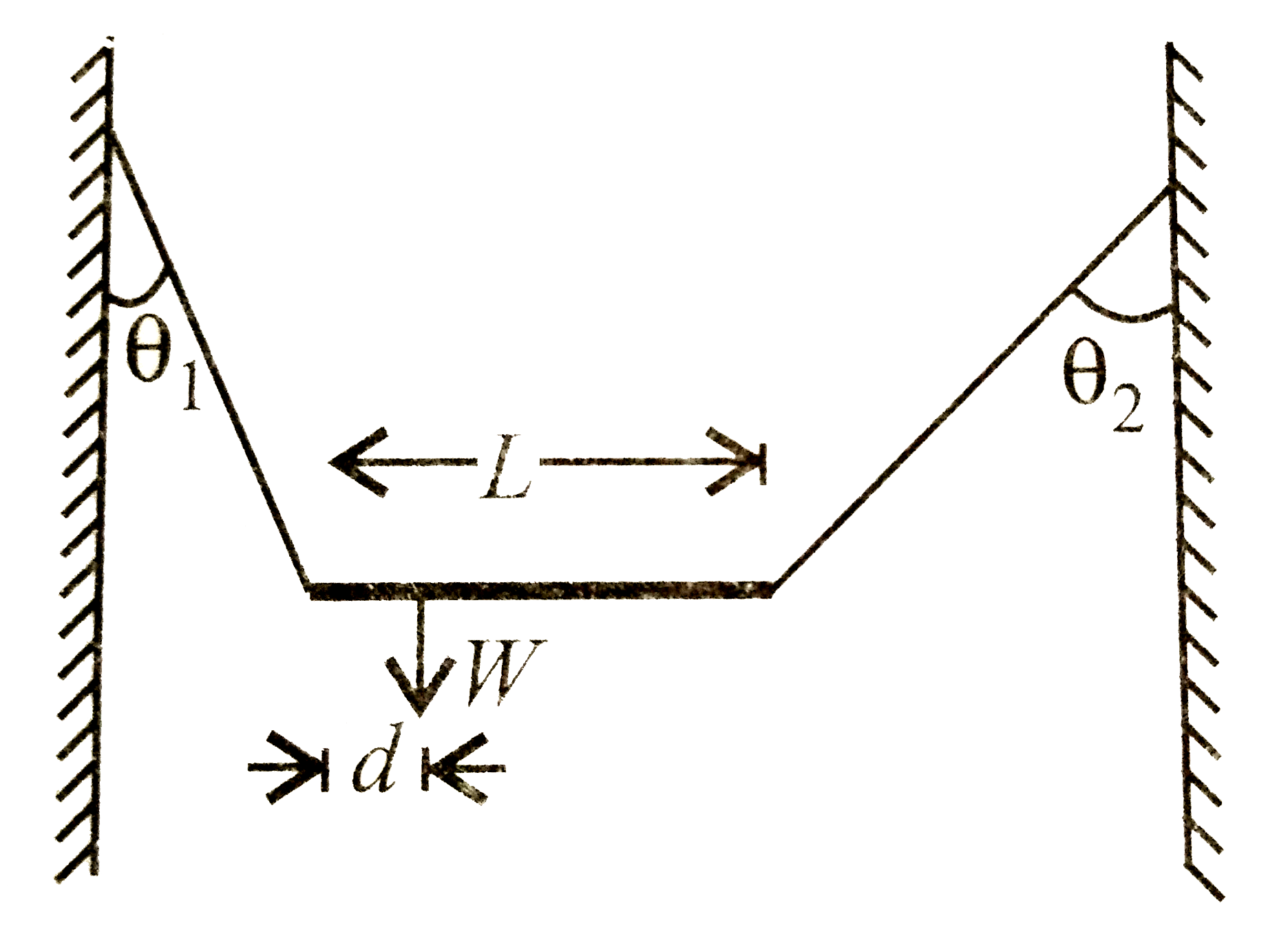
View SolutionA non-uniform bar weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from its left end is
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View SolutionA uniform square plate of mass m is supported with its plane vertical as shown in the figure. Assume the centre of mass is on a horizontal the passing through A. If the cable at B breaks then just after that the angular acceleration of the plate is
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View Solution
A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View Solution
