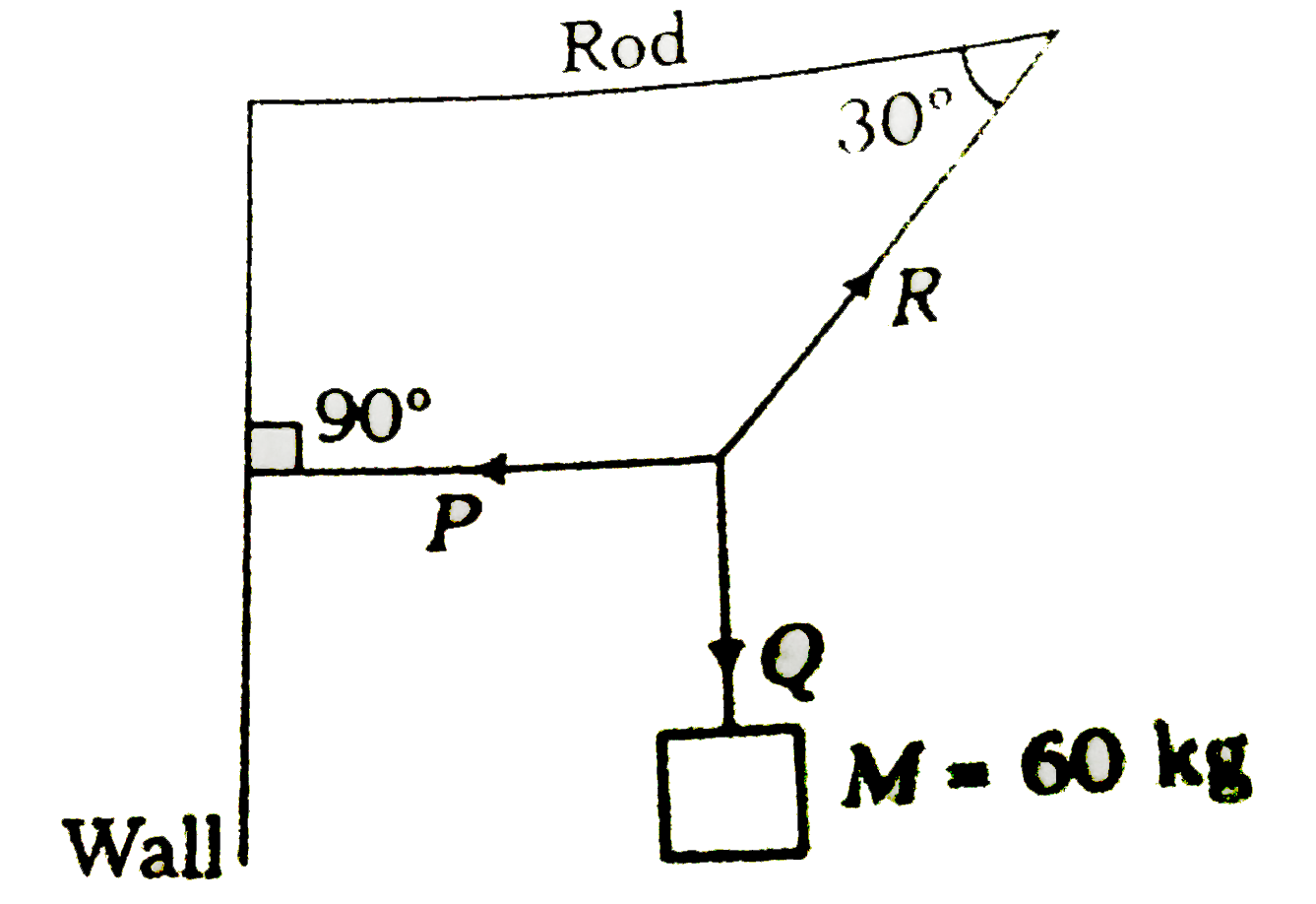
A body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
130.9 kgf
60 kgf
50 kgf
103.9 kgf
The correct Answer is:D
(d) The given figure can be drawn as

Taking component of forces
Rcosθ=Mg⇒Rcos60∘=Mg….(i)
and Rsin60∘=T ….…(ii)
By Eqs. (i) and (ii), we get
⇒tan60∘=TMg⇒T=Mgtan60∘
or T=60×g×√3=103.9kgf
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.320videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.420videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.120videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A mass M of 100 kg is suspended with the use of strings A, B 90 and C as shown in the figure, where W is the vertical wall and R is a rigid horizontal rod. The tension in the string B is
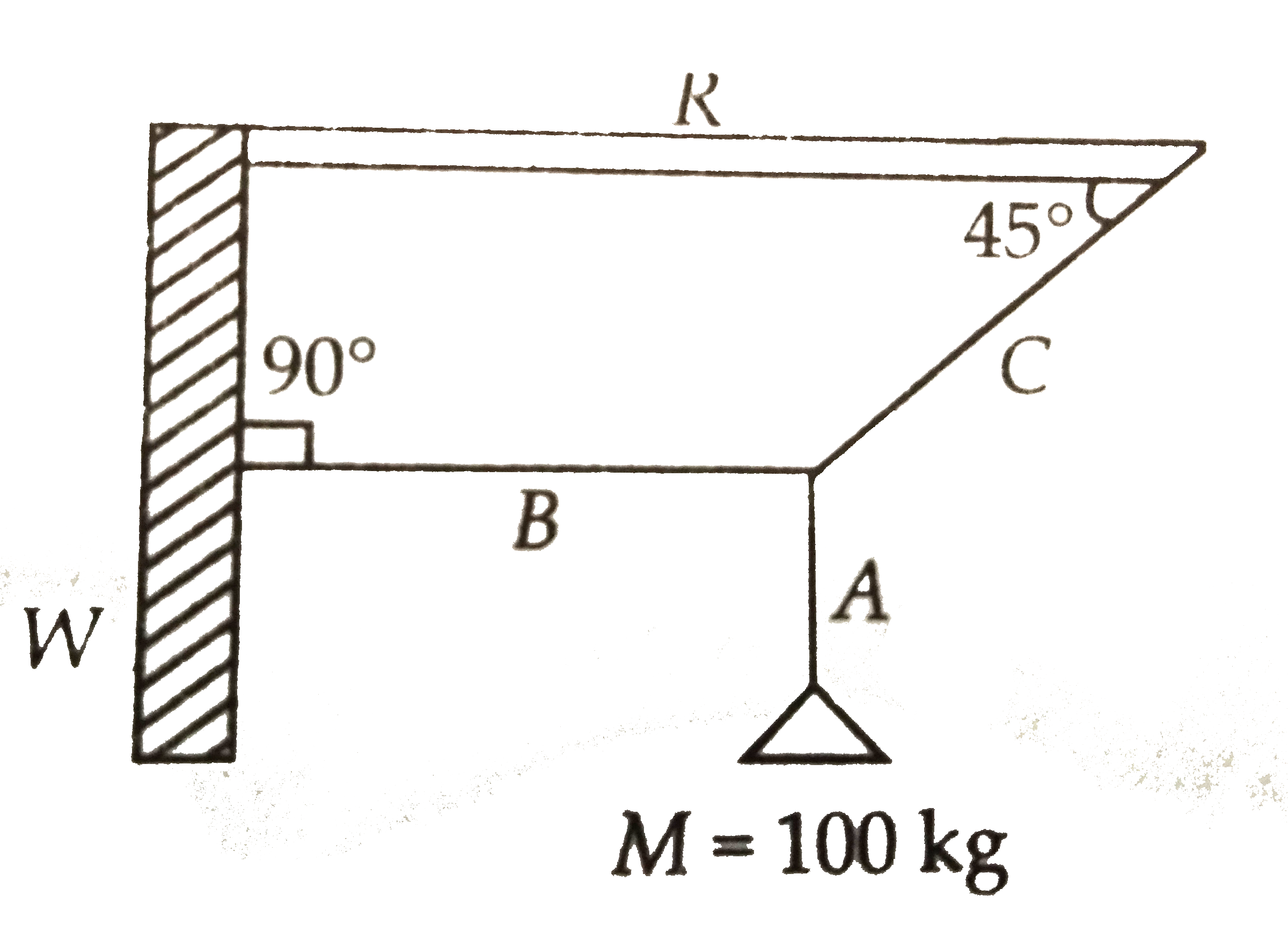 A100g NBzeroC100√2gND100√2gN
A100g NBzeroC100√2gND100√2gN
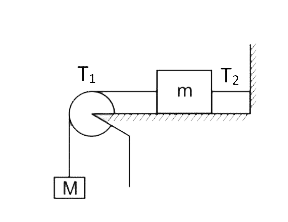
For the system shown in figure, the tensions in the string
 View Solution
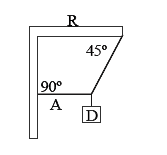
View SolutionA blolck D weighing 300kg is suspended by means of two cords A and B as shown in the figure. W is a vertical wall and R a horizontal rigid beam. The tension in the string A in kg is :
 View Solution
View SolutionFind the tension in the strings AC and BC shown in figure.
 View Solution
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is
 View Solution
View SolutionThe tension T in the string shown in figure is
 View Solution
View SolutionA block of mass 3m is suspended by a meter scale rod of mass m as shown in figure. If the tension in the string A is equal to kmg in equilibrium, then value of k will be
 View Solution
View Solution



