Consider a block connected to a light spring of spring constant 100Nm−1. Now the block is displaced by applying a constant force F which gives zero resultant force when spring is stretched through 10 cm. 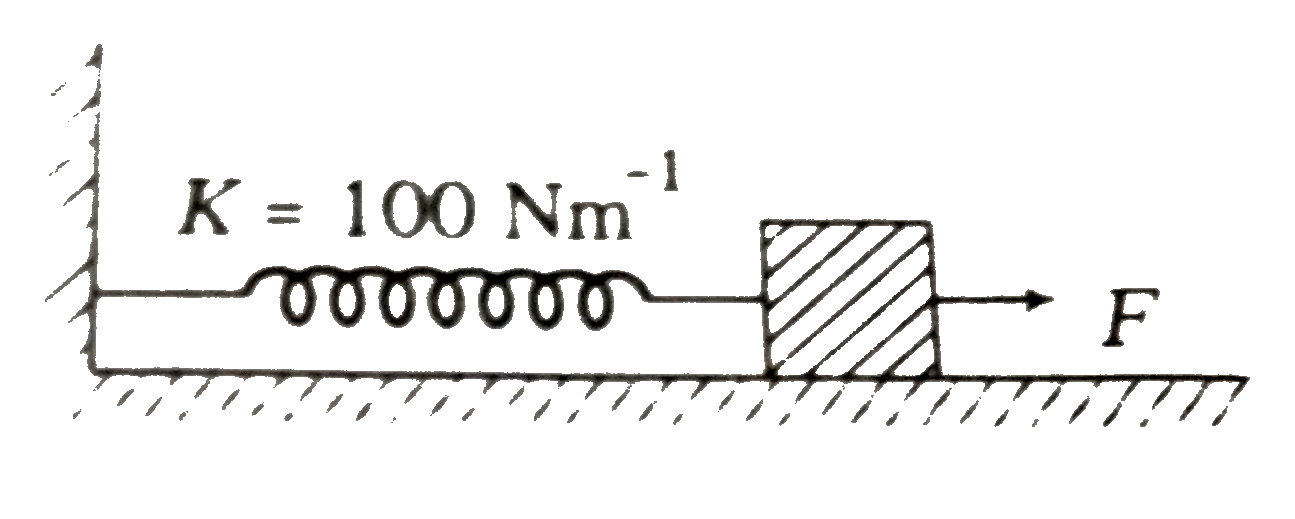
Evaluate
(i) Work done by the spring force when the block attains equilibrium.
(ii) Net work done on the block when it attains maximum speed.
(i) Work done by the spring force, W=12kx2
k=100Nm−1 and x=10cm=0.1m
∴Ws=12×100(0.1)2=−0.5J
Negative sign indicates that the work done by the spring force is negative.
(ii) When the block attains equilibrium, its speed is maximum.
∴ Work done on the block by external force F
W=F.x=(10)(10100)=1J
Thus, net work done on the block
WN=WS+W=−0.5+1=0.5J
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.1
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied hrizontally towards right. The maximum speed of the block will be (there is no friction between block and the surface)

View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View Solution
Knowledge Check
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
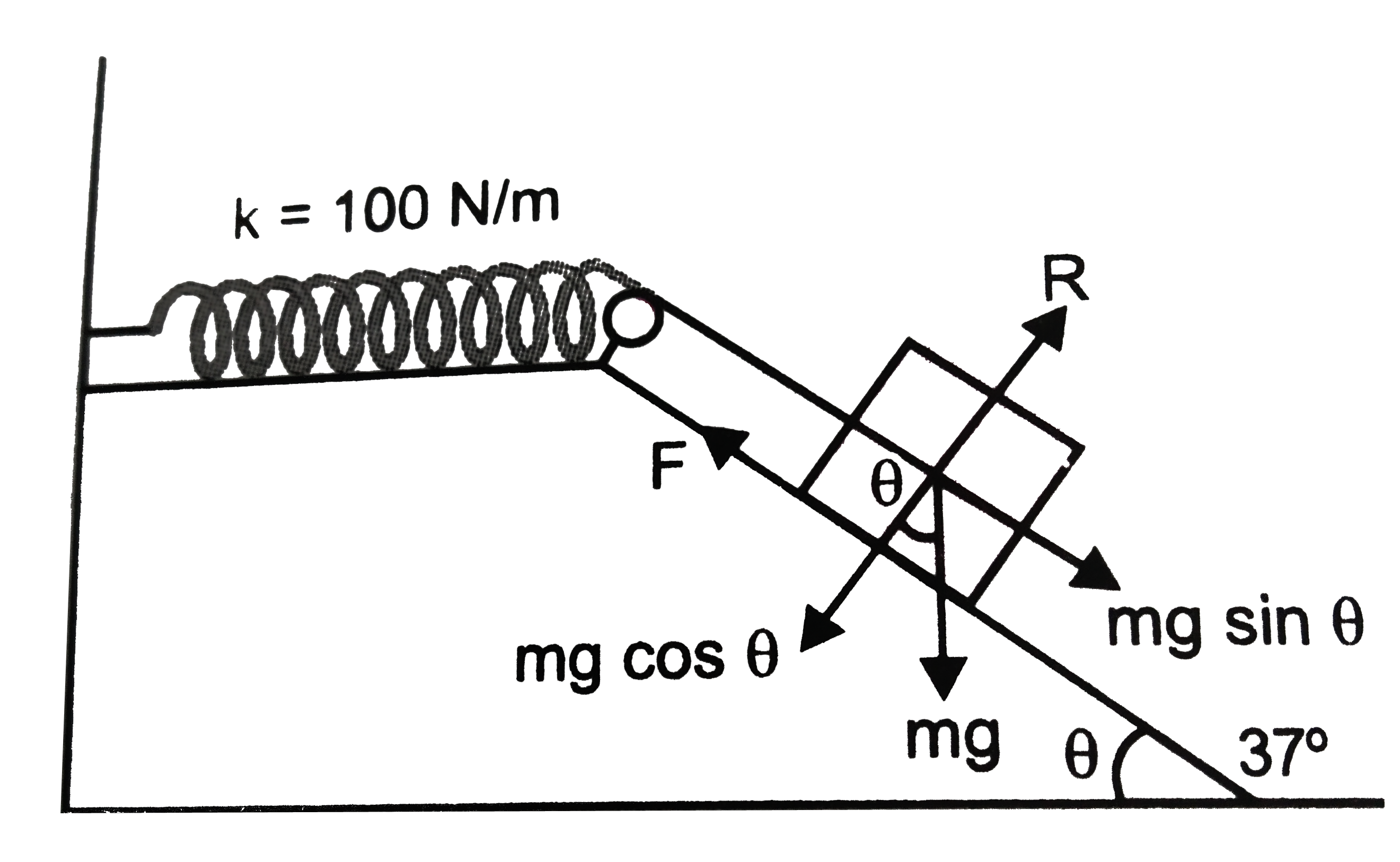 A0.2B0.3C0.5D0.6
A0.2B0.3C0.5D0.6
A block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
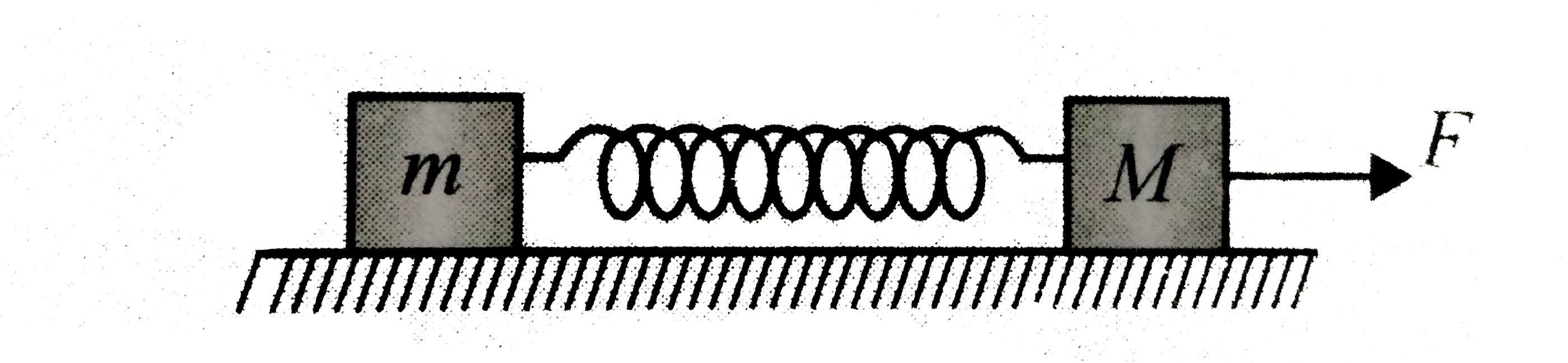
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionA 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.

View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionA spring 40 mm long is stretched by the application of a force. If 10 N force required to stretch the spring through 1mm, then the work done in stretching the spring through 40 mm is
View Solution
