A force F=kx (where k is a positive constant) is acting on a particle Work done:
Column-1 Column-2(A)in displacing the body from x=2 to x=4(P) Negative(B)In displacing the body from x=-4 to x=-2(Q) Positive(C)In displacing the body from x=-2 to x=+2(R) Zero
The correct Answer is:(A→q,B→p,C→r)
To solve the problem, we need to calculate the work done by the force F=kx for three different displacements. The work done W by a force is given by the integral of the force over the displacement.
1. Understanding the Force:
The force acting on the particle is given by F=kx, where k is a positive constant.
2. Work Done Formula:
The work done W by a variable force is calculated using the integral:
W=∫Fdx
Substituting the expression for F:
W=∫kxdx
3. Calculating Work Done from x=2 to x=4:
W=∫42kxdx=k∫42xdx
The integral of x is:
∫xdx=x22
Therefore,
W=k(x22)42=k(422−222)=k(162−42)=k(8−2)=6k
Since k is positive, W=6k>0. Thus, this corresponds to option (A) matching with (Q).
4. Calculating Work Done from x=−4 to x=−2:
W=∫−2−4kxdx=k∫−2−4xdx
Using the same integral:
W=k(x22)−2−4=k((−2)22−(−4)22)=k(42−162)=k(2−8)=−6k
Since k is positive, W=−6k<0. Thus, this corresponds to option (B) matching with (P).
5. Calculating Work Done from x=−2 to x=2:
W=∫2−2kxdx=k∫2−2xdx
The integral of x over symmetric limits around zero results in zero:
W=k(x22)2−2=k(222−(−2)22)=k(42−42)=k(2−2)=0
Thus, this corresponds to option (C) matching with (R).
Summary of Results:
- (A) Work done from x=2 to x=4: Positive (matches with Q)
- (B) Work done from x=−4 to x=−2: Negative (matches with P)
- (C) Work done from x=−2 to x=2: Zero (matches with R)
The force acting on the particle is given by F=kx, where k is a positive constant.
The work done W by a variable force is calculated using the integral:
W=∫Fdx
Substituting the expression for F:
W=∫kxdx
W=∫42kxdx=k∫42xdx
The integral of x is:
∫xdx=x22
Therefore,
W=k(x22)42=k(422−222)=k(162−42)=k(8−2)=6k
Since k is positive, W=6k>0. Thus, this corresponds to option (A) matching with (Q).
W=∫−2−4kxdx=k∫−2−4xdx
Using the same integral:
W=k(x22)−2−4=k((−2)22−(−4)22)=k(42−162)=k(2−8)=−6k
Since k is positive, W=−6k<0. Thus, this corresponds to option (B) matching with (P).
W=∫2−2kxdx=k∫2−2xdx
The integral of x over symmetric limits around zero results in zero:
W=k(x22)2−2=k(222−(−2)22)=k(42−42)=k(2−2)=0
Thus, this corresponds to option (C) matching with (R).
- (A) Work done from x=2 to x=4: Positive (matches with Q)
- (B) Work done from x=−4 to x=−2: Negative (matches with P)
- (C) Work done from x=−2 to x=2: Zero (matches with R)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS16videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
Similar Questions
A force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
View SolutionThe relationship between force and position is shown in fig ( in one dimensional case). The work done in displacing a body from x=1cm to x = 5 cm is:
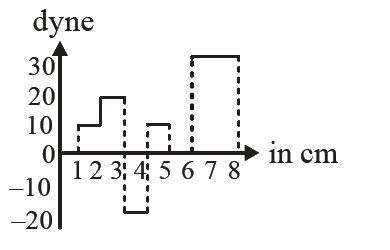 View Solution
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View Solution

