Average velocity of a particle executing SHM in one complete vibration is :
ω2A2
ω2A√2
zero
Aω2
The correct Answer is:C
To find the average velocity of a particle executing simple harmonic motion (SHM) in one complete vibration, we can follow these steps:
1. Understand the Motion:
- A particle in SHM moves back and forth around an equilibrium position. The displacement can be described by the equation:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
2. Find the Velocity:
- The velocity v(t) of the particle is the derivative of displacement x(t) with respect to time t:
v(t)=dxdt=Aωcos(ωt+ϕ)
3. Average Velocity Over One Complete Cycle:
- To find the average velocity over one complete cycle, we need to integrate the velocity over one period T and then divide by the period:
Average Velocity=1T∫T0v(t)dt
- Since the velocity function v(t)=Aωcos(ωt+ϕ) oscillates between positive and negative values, we can analyze its behavior over one complete cycle.
4. Evaluate the Integral:
- The average value of the cosine function over one complete cycle is zero:
∫T0cos(ωt+ϕ)dt=0
- Therefore, the average velocity becomes:
Average Velocity=1T⋅0=0
5. Conclusion:
- The average velocity of a particle executing SHM in one complete vibration is:
Average Velocity=0
Final Answer:
The average velocity of a particle executing SHM in one complete vibration is 0.
---
- A particle in SHM moves back and forth around an equilibrium position. The displacement can be described by the equation:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
- The velocity v(t) of the particle is the derivative of displacement x(t) with respect to time t:
v(t)=dxdt=Aωcos(ωt+ϕ)
- To find the average velocity over one complete cycle, we need to integrate the velocity over one period T and then divide by the period:
Average Velocity=1T∫T0v(t)dt
- Since the velocity function v(t)=Aωcos(ωt+ϕ) oscillates between positive and negative values, we can analyze its behavior over one complete cycle.
- The average value of the cosine function over one complete cycle is zero:
∫T0cos(ωt+ϕ)dt=0
- Therefore, the average velocity becomes:
Average Velocity=1T⋅0=0
- The average velocity of a particle executing SHM in one complete vibration is:
Average Velocity=0
The average velocity of a particle executing SHM in one complete vibration is 0.
Similar Questions
Knowledge Check
When the displacement of a particle executing SHM is one-fourth of its amplitude, what fraction of the total energy is the kinetic energy?
A1615B1516C34D43
The maximum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
View Solution
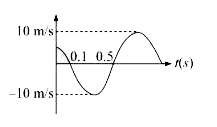
The variation of velocity of a particle executing SHM with time is shown is fig. The velocity of the particle when a phase change of π6 takes place from the instant it is at one of the extreme positions will be
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
View SolutionIf the displacement (x) and velocity (v) of a particle executing SHM are related through the expression 3v2=30−x2. If the time period of the particle is T=π√n, then what is the value of n?
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
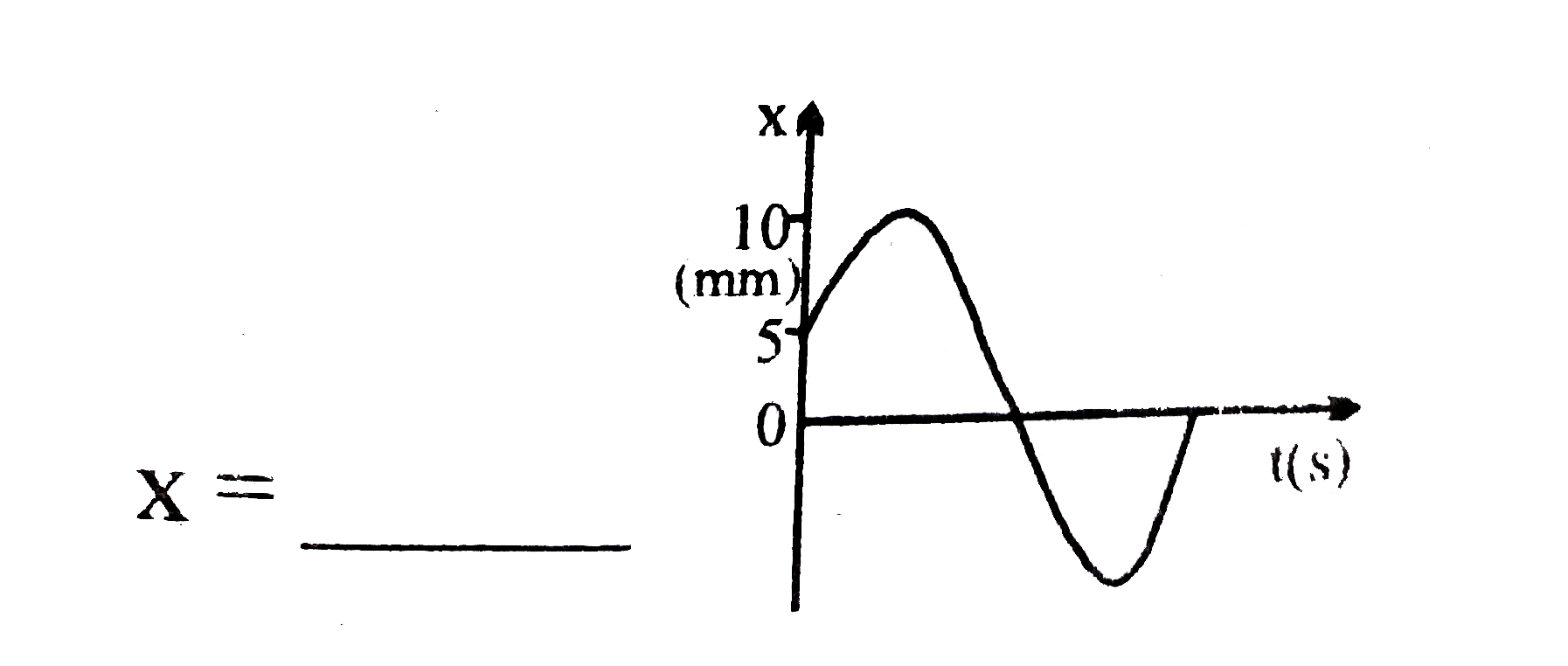
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
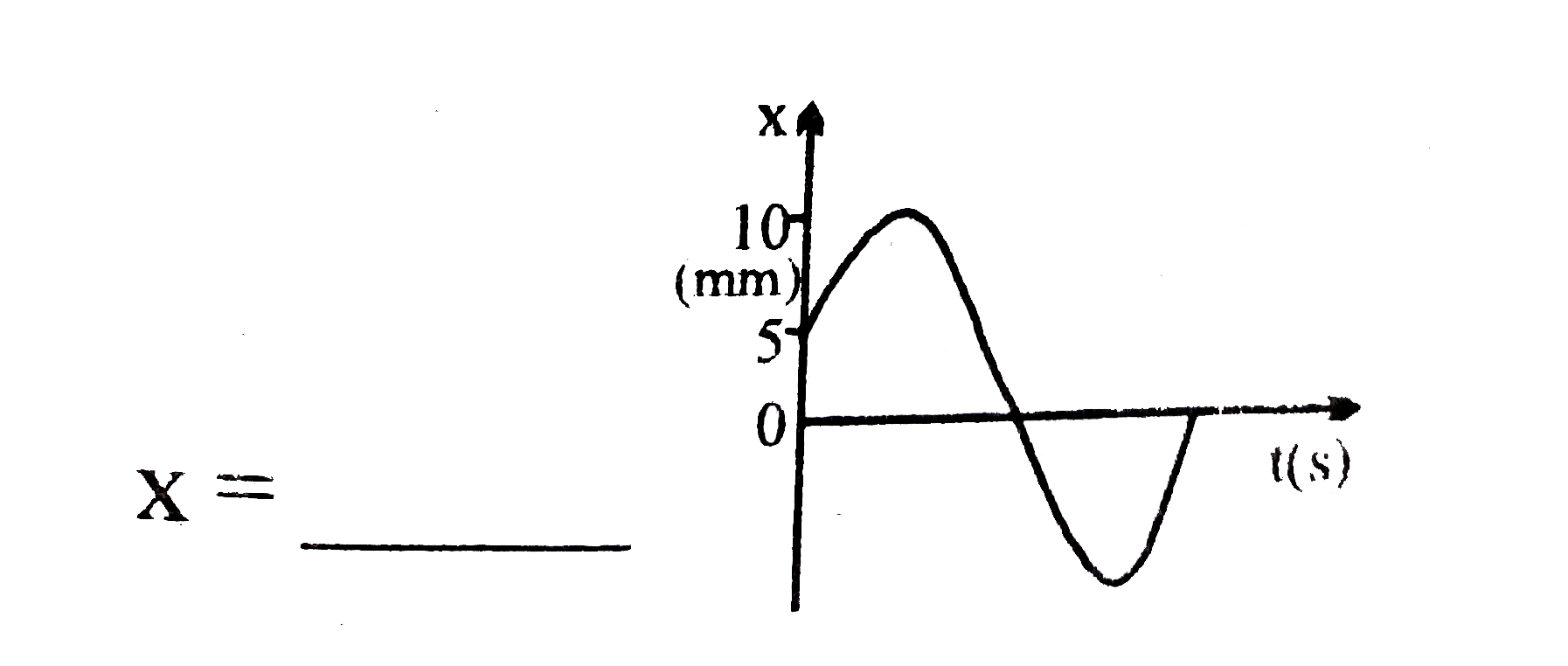
View SolutionVelocity at mean position of a particle executing SHM is v. Velocity of the particle at a distance equal to half of the amplitude will be
View Solution
