The maximum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
(a)0.01 s
(b)10 s
(c)0.1 s
(d)100 s
The correct Answer is:A
To find the period of oscillation for a particle executing simple harmonic motion (SHM) with a given amplitude and maximum velocity, we can follow these steps:
Step 1: Understand the relationship between maximum velocity, amplitude, and angular frequency
The maximum velocity (V_max) in SHM is given by the formula:
Vmax=A⋅ω
where:
- Vmax is the maximum velocity,
- A is the amplitude,
- ω is the angular frequency.
Step 2: Convert the amplitude to meters
The amplitude is given as 7 mm. We need to convert this to meters:
A=7mm=7×10−3m
Step 3: Substitute the known values into the formula
We know:
- Vmax=4.4m/s
- A=7×10−3m
Substituting these values into the maximum velocity formula:
4.4=(7×10−3)⋅ω
Step 4: Solve for angular frequency (ω)
Rearranging the equation to solve for ω:
ω=4.47×10−3
Calculating ω:
ω=4.40.007≈628.57rad/s
Step 5: Relate angular frequency to the period
The angular frequency ω is related to the period T by the formula:
ω=2πT
Step 6: Solve for the period (T)
Rearranging the equation to solve for T:
T=2πω
Substituting the value of ω:
T=2π628.57
Calculating T:
T≈6.2832628.57≈0.01s
Final Answer
The period of oscillation is approximately:
T≈0.01s
---
The maximum velocity (V_max) in SHM is given by the formula:
Vmax=A⋅ω
where:
- Vmax is the maximum velocity,
- A is the amplitude,
- ω is the angular frequency.
The amplitude is given as 7 mm. We need to convert this to meters:
A=7mm=7×10−3m
We know:
- Vmax=4.4m/s
- A=7×10−3m
4.4=(7×10−3)⋅ω
Rearranging the equation to solve for ω:
ω=4.47×10−3
ω=4.40.007≈628.57rad/s
The angular frequency ω is related to the period T by the formula:
ω=2πT
Rearranging the equation to solve for T:
T=2πω
T=2π628.57
T≈6.2832628.57≈0.01s
The period of oscillation is approximately:
T≈0.01s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (2)
Explore 40 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
The maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
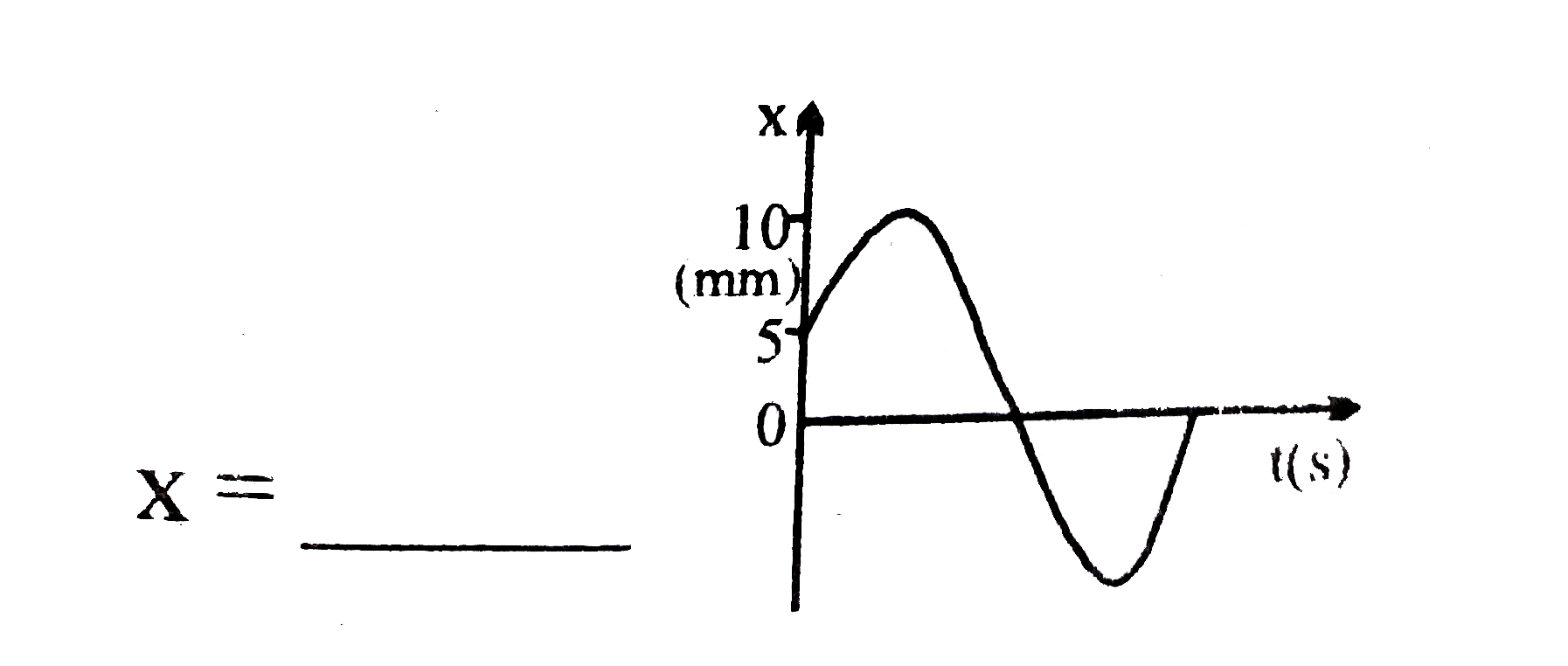
View Solution
Knowledge Check
The maximum velocity of a particle executing simple harmonic motion is v. If the amplitude is doubled and the time period of oscillation decreased to 1/3 of its original value the maximum velocity becomes
A18vB12vC6vD3vThe kinetic energy of a particle, executing S.H.M. is 16 J when it is in its mean position. IF the amplitude of oscillation is 25 cm and the mass of the particle is 5.12 Kg, the time period of its oscillations is
Aπ/5 secB2πsecC20πsecD5π sec
The figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
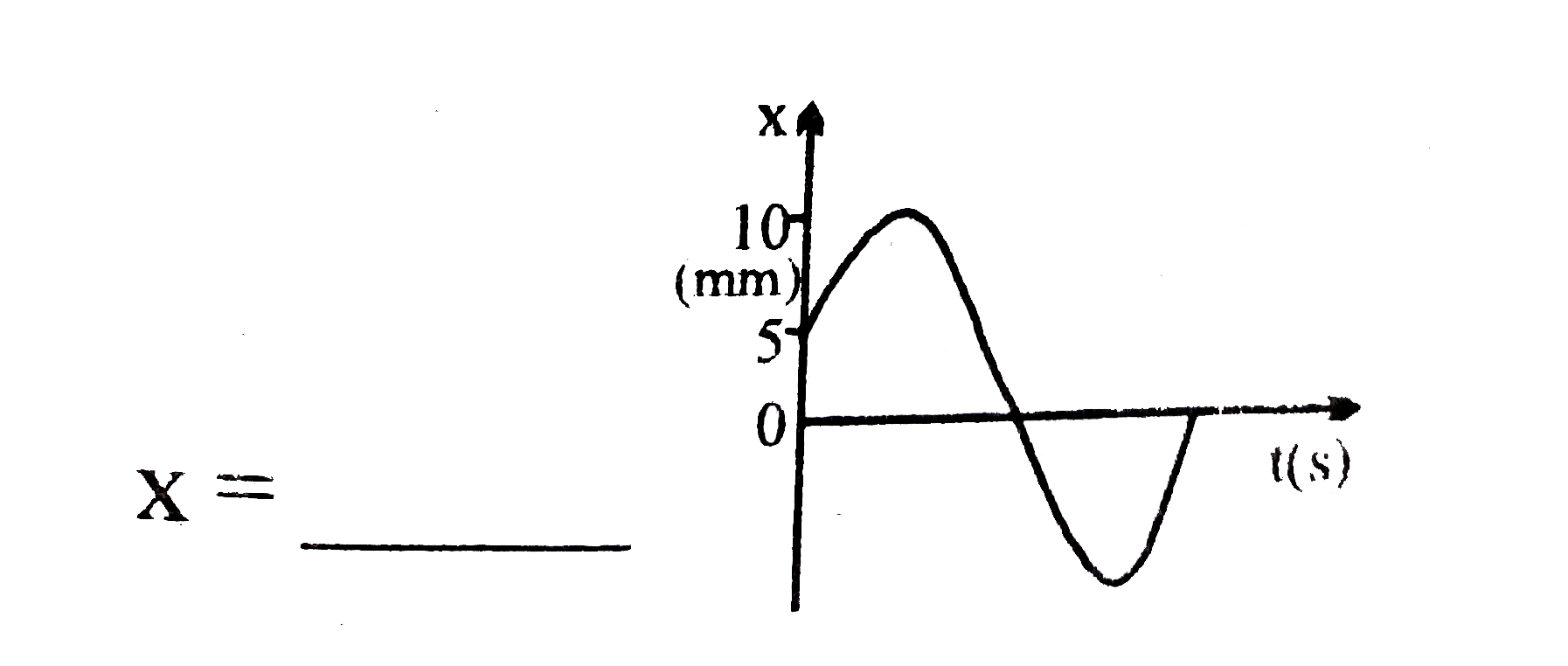
View SolutionThe amplitude of a particle executing SHM about O is 10cm. Then
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
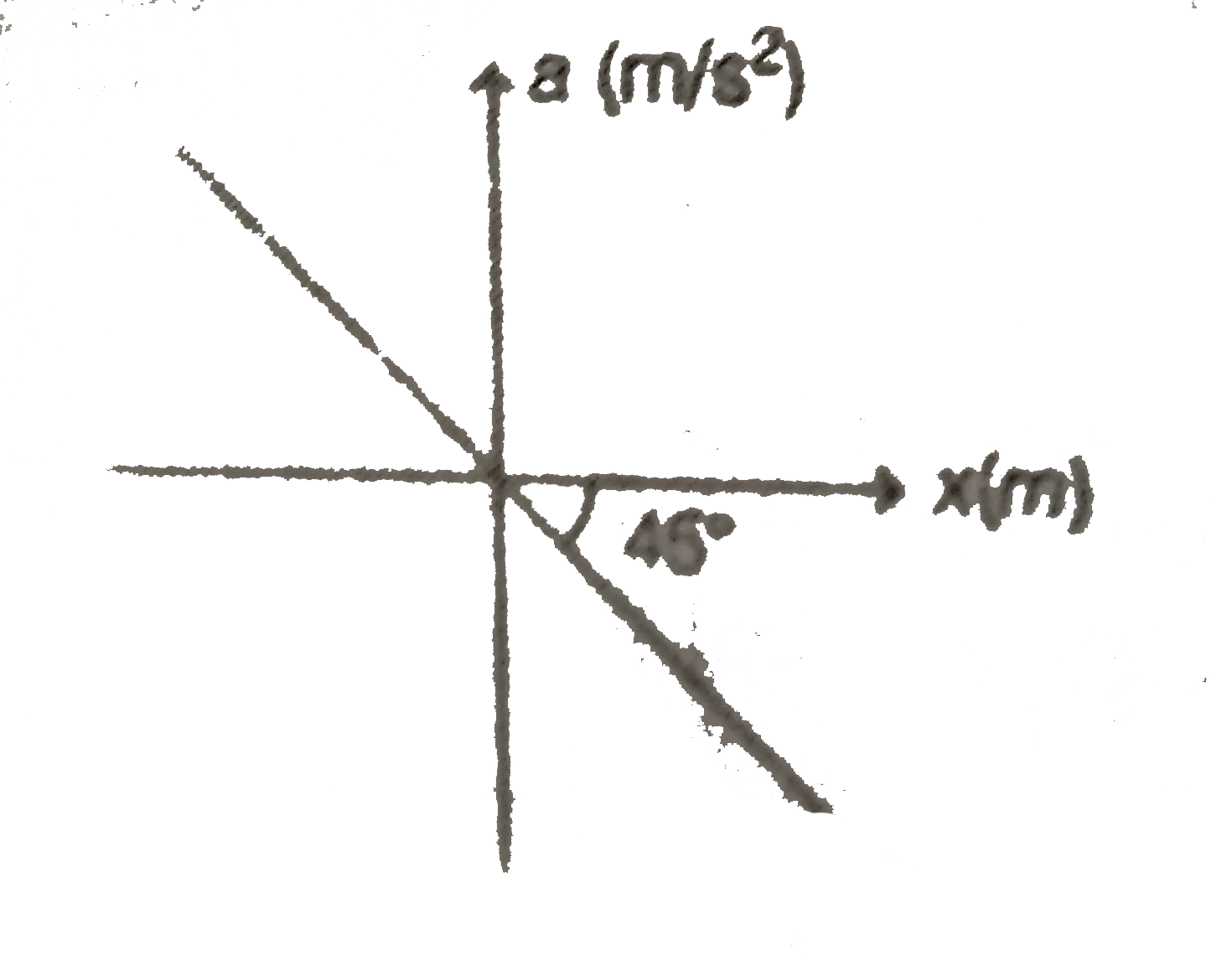
View SolutionIf the maximum speed and acceleration of a particle executing SHM is 20cm/sand100πcm/s2, find the time period od oscillation.
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View SolutionThe potential energy of a particle executing SHM change from maximum to minimum in 5s. Then the time period of SHM is:
View Solution
