If the displacement (x) and velocity (v) of a particle executing SHM are related through the expression 3v2=30−x2. If the time period of the particle is T=π√n, then what is the value of n?
The correct Answer is:12.00
To solve the problem, we start with the given expression relating the displacement x and velocity v of a particle executing simple harmonic motion (SHM):
3v2=30−x2
Step 1: Express v2 in terms of x
From the equation, we can isolate v2:
v2=30−x23
Step 2: Use the formula for velocity in SHM
In SHM, the velocity v can also be expressed in terms of angular frequency ω and amplitude A:
v2=ω2(A2−x2)
Step 3: Set the two expressions for v2 equal to each other
Now we can set the two expressions for v2 equal:
30−x23=ω2(A2−x2)
Step 4: Rearrange the equation
Multiplying both sides by 3 to eliminate the fraction:
30−x2=3ω2(A2−x2)
Expanding the right side:
30−x2=3ω2A2−3ω2x2
Step 5: Collect like terms
Rearranging gives us:
30=3ω2A2+(3ω2−1)x2
Step 6: Identify constants
For this equation to hold for all x, the coefficient of x2 must be zero (since the left side is a constant). Therefore, we set:
3ω2−1=0
Solving for ω2:
3ω2=1⟹ω2=13
Step 7: Find ω
Taking the square root:
ω=1√3
Step 8: Relate ω to the time period T
The time period T is related to ω by the formula:
T=2πω
Substituting ω:
T=2π1√3=2π√3
Step 9: Compare with the given time period
The problem states that T=π√n. Setting the two expressions for T equal:
2π√3=π√n
Step 10: Solve for n
Dividing both sides by π:
2√3=√n
Squaring both sides:
4⋅3=n⟹n=12
Thus, the value of n is:
12
Similar Questions
The displacement (x) is plotted with time (t) for a particle executing SHM as shown below. The correct equation of SHM is

View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionVariation of acceleration a of a particle executing SHM with displacement x is
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionA particle is executing SHM with time period T. If time period of its total mechanical energy isT' then T'T is
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
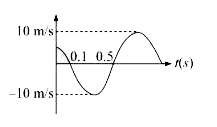
View SolutionA particle executing SHM of amplitude a has displace ment a2 at t=T4 and a negative velocity. The epoch of the particle is
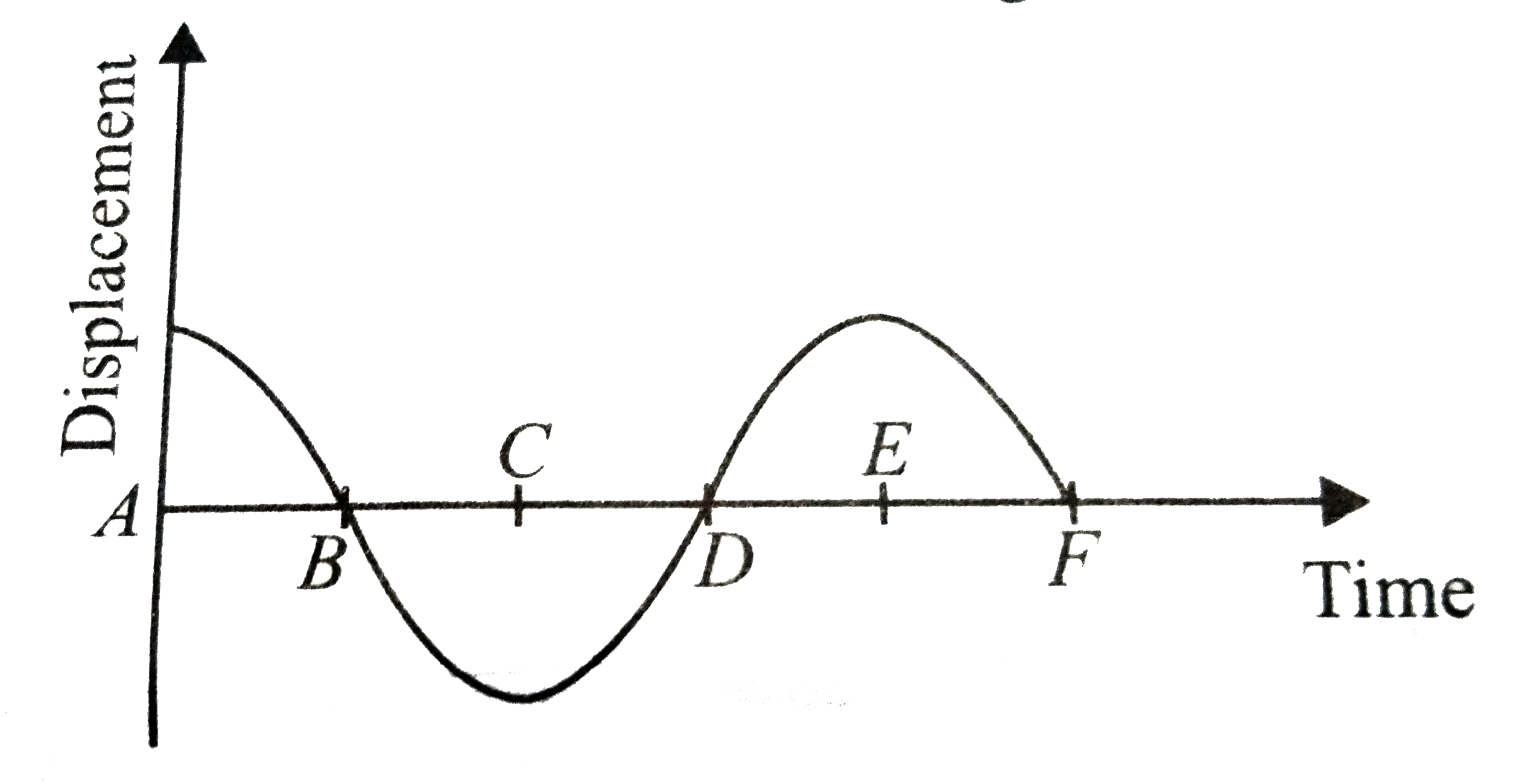
View Solutiondisplacement versus time curve for a particle executing SHM is is as shown in figure. At what points the velocity of the particle is zero?
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
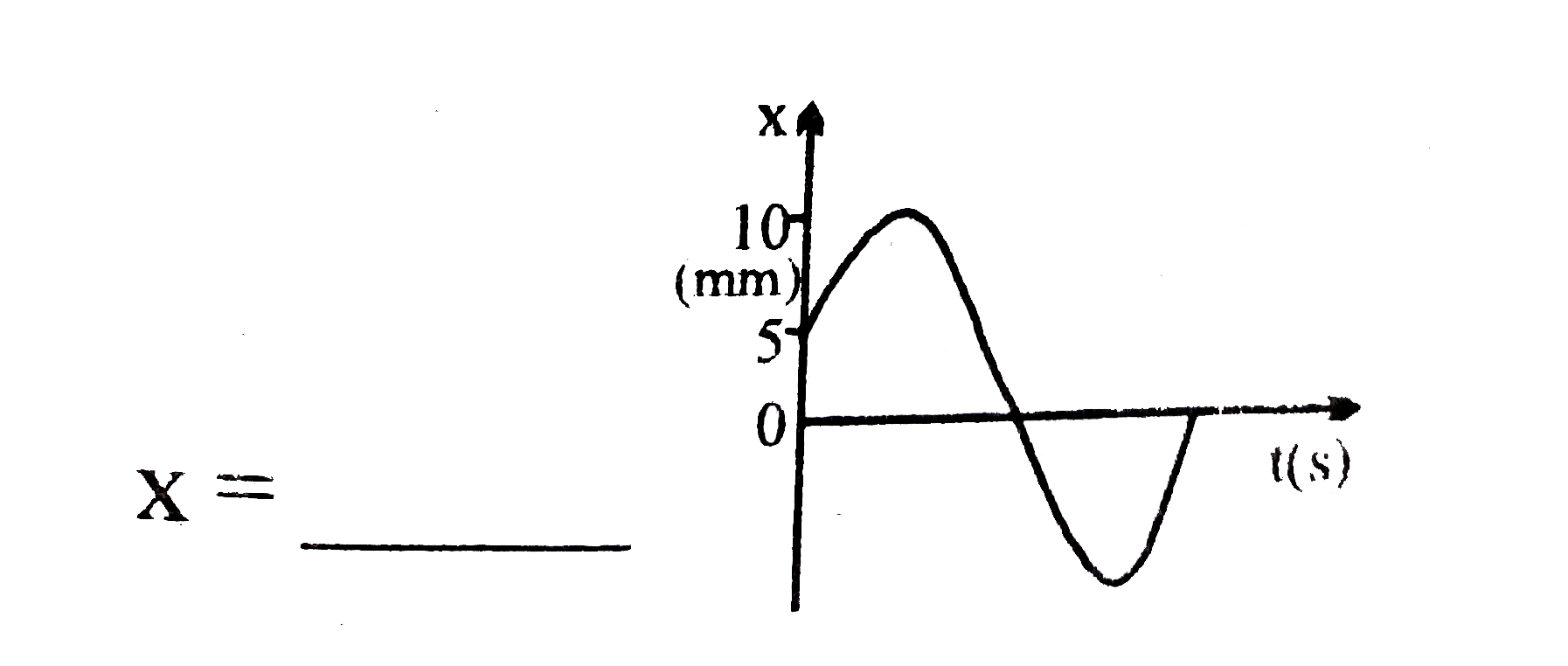
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
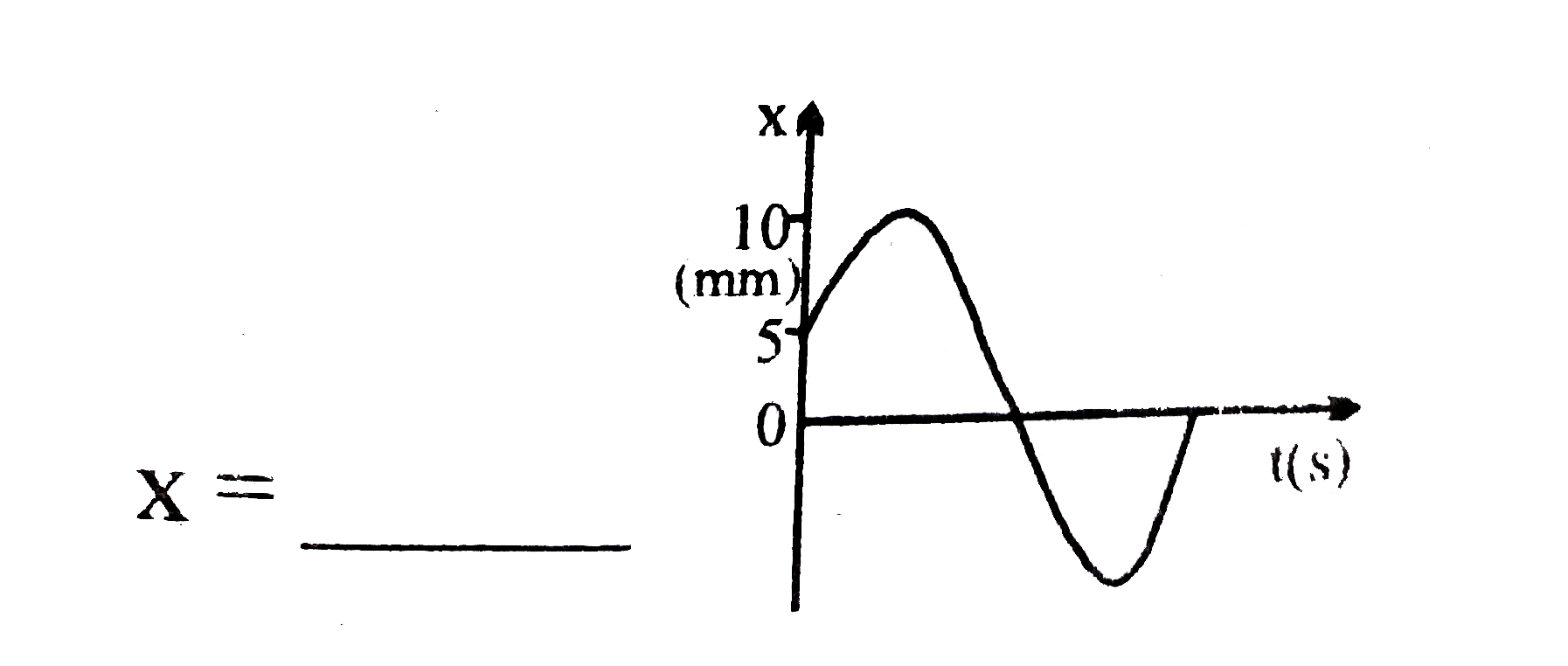
View Solution
