A container has a small hole at its bottom. Area of cross-section of the hole is A1 and that of the container is A2. Liquid is poured in the container at a constant rate Qm3s−1. The maximum level of liquid in the container will be
Q22gA1A2
Q22gA21
Q2gA1A2
Q22gA2^(2)
The correct Answer is:B
To solve the problem, we need to find the maximum height of liquid in the container when the rate of inflow equals the rate of outflow. Here’s a step-by-step solution:
Step 1: Understand the problem
We have a container with a hole at the bottom. Liquid is being poured into the container at a constant rate Q (in m3/s). The cross-sectional area of the hole is A1 and the cross-sectional area of the container is A2. We need to find the maximum height hmax of the liquid in the container.
Step 2: Set up the inflow and outflow rates
The inflow rate of the liquid into the container is given as Q (in m3/s). The outflow rate through the hole can be expressed using Torricelli’s law, which states that the velocity of efflux v of a fluid under the influence of gravity is given by:
v=√2gh
where g is the acceleration due to gravity and h is the height of the liquid above the hole.
Step 3: Write the outflow rate
The outflow rate Qout through the hole can be calculated as:
Qout=A1⋅v=A1⋅√2gh
Step 4: Set inflow equal to outflow
At maximum height, the inflow rate equals the outflow rate:
Q=A1⋅√2ghmax
Step 5: Solve for hmax
Rearranging the equation to solve for hmax:
√2ghmax=QA1
Squaring both sides gives:
2ghmax=(QA1)2
Now, isolate hmax:
hmax=Q22gA21
Conclusion
The maximum height of the liquid in the container is given by:
hmax=Q22gA21
We have a container with a hole at the bottom. Liquid is being poured into the container at a constant rate Q (in m3/s). The cross-sectional area of the hole is A1 and the cross-sectional area of the container is A2. We need to find the maximum height hmax of the liquid in the container.
The inflow rate of the liquid into the container is given as Q (in m3/s). The outflow rate through the hole can be expressed using Torricelli’s law, which states that the velocity of efflux v of a fluid under the influence of gravity is given by:
v=√2gh
where g is the acceleration due to gravity and h is the height of the liquid above the hole.
The outflow rate Qout through the hole can be calculated as:
Qout=A1⋅v=A1⋅√2gh
At maximum height, the inflow rate equals the outflow rate:
Q=A1⋅√2ghmax
Rearranging the equation to solve for hmax:
√2ghmax=QA1
Squaring both sides gives:
2ghmax=(QA1)2
Now, isolate hmax:
hmax=Q22gA21
The maximum height of the liquid in the container is given by:
hmax=Q22gA21
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A tank has a hole at its bottom. The time needed to empty the tank from level h1 to h2 will be proportional to
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
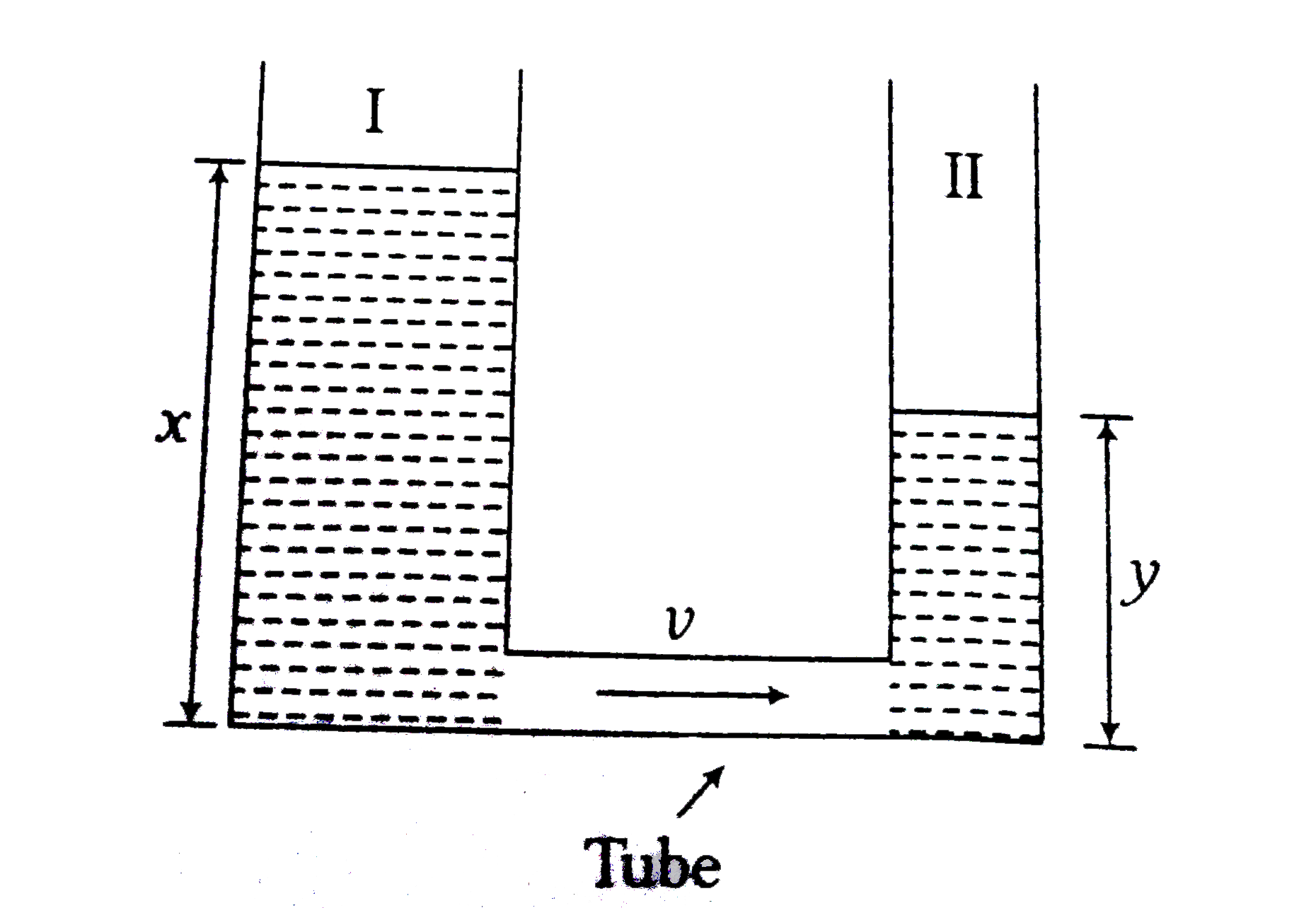
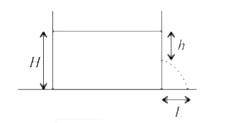
View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
View Solution0.5mol of H2, SO2, and CH4 is kept in a container. A hole was made in the container. After 3hours, the order of partial pressure in the container will be
View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case

View SolutionA hollow cylindrical container floats in water with half its length immersed. A liquid of specific gravity σ is slowly poured into the container until the levels of the liquid inside the container and of water outside are the same. It is observed that the container is submerged to two-thirds its length. Then the value of σ is
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionA sufficiently long closed organ pipe has a small hole at its bottom. Initially the pipe is empty. What poured into the pipe at a constant rate. The fundamental frequency of the air column in the pite
View SolutionA large open top container of negligible mass and uniform cross sectional area A a has a small hole of cross sectional area A/100 in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density ρ and mass M0. Assuming that the liquid starts flowing out horizontally through the hole at t=0, calculate a the acceleration of the container and its velocity when 75% of the liquid has drained out.
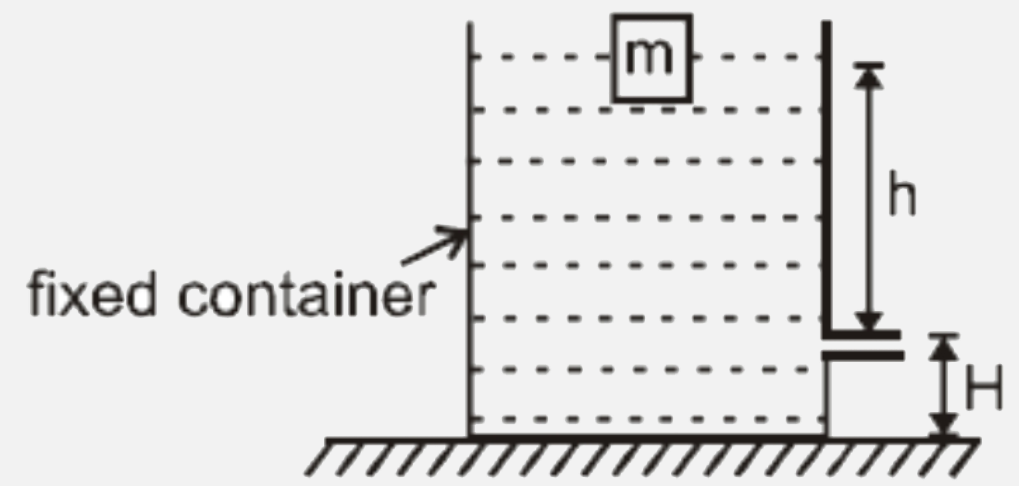
View SolutionIf the pin hole in the container is very small compared to the area of the base of container and a block floats in the ideal liquid then, the speed of efflux is
View Solution
