A magnetic needle is free to oscillate in a uniform magnetic field as shown in the figure. The magnetic moment of magnetic needle 7.2Am2 and moment of inertia I=6.5×10−6kgm2. The number of oscillation performed in 5s are 10. Calculate the magnitude of magnetic field?
To solve the problem, we need to calculate the magnitude of the magnetic field B using the given parameters of the magnetic needle. Here are the steps to solve the problem:
Step 1: Determine the Time Period of Oscillation
The number of oscillations performed in 5 seconds is given as 10. Therefore, the time period T can be calculated as:
T=Total timeNumber of oscillations=5 s10=0.5 s
Step 2: Use the Formula for Time Period of a Magnetic Needle
The formula for the time period T of a magnetic needle oscillating in a magnetic field is given by:
T=2π√ImB
Where:
- I = moment of inertia of the needle
- m = magnetic moment of the needle
- B = magnetic field strength
Step 3: Rearranging the Formula to Solve for B
We can rearrange the formula to solve for B:
B=4π2ImT2
Step 4: Substitute the Known Values
Now we can substitute the known values into the equation:
- I=6.5×10−6kg m2
- m=7.2A m2
- T=0.5s
Substituting these values gives:
B=4π2(6.5×10−6)7.2×(0.5)2
Step 5: Calculate T2
Calculating T2:
T2=(0.5)2=0.25s2
Step 6: Substitute T2 into the Equation
Now substituting T2 back into the equation for B:
B=4π2(6.5×10−6)7.2×0.25
Step 7: Calculate the Value of B
Calculating the denominator:
7.2×0.25=1.8
Now substituting this back into the equation:
B=4π2(6.5×10−6)1.8
Calculating 4π2:
4π2≈39.478
Now substituting this value:
B=39.478×(6.5×10−6)1.8
Calculating the numerator:
39.478×6.5≈256.609
Now substituting:
B=256.609×10−61.8≈142.56×10−6T
Final Answer
Thus, the magnitude of the magnetic field B is approximately:
B≈141.55μT
The number of oscillations performed in 5 seconds is given as 10. Therefore, the time period T can be calculated as:
T=Total timeNumber of oscillations=5 s10=0.5 s
The formula for the time period T of a magnetic needle oscillating in a magnetic field is given by:
T=2π√ImB
Where:
- I = moment of inertia of the needle
- m = magnetic moment of the needle
- B = magnetic field strength
We can rearrange the formula to solve for B:
B=4π2ImT2
Now we can substitute the known values into the equation:
- I=6.5×10−6kg m2
- m=7.2A m2
- T=0.5s
B=4π2(6.5×10−6)7.2×(0.5)2
Calculating T2:
T2=(0.5)2=0.25s2
Now substituting T2 back into the equation for B:
B=4π2(6.5×10−6)7.2×0.25
Calculating the denominator:
7.2×0.25=1.8
Now substituting this back into the equation:
B=4π2(6.5×10−6)1.8
4π2≈39.478
Now substituting this value:
B=39.478×(6.5×10−6)1.8
39.478×6.5≈256.609
Now substituting:
B=256.609×10−61.8≈142.56×10−6T
Thus, the magnitude of the magnetic field B is approximately:
B≈141.55μT
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.115videos
MAGNETISM AND MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.215videos
MAGNETISM AND MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions17videos
MODERN PHYSICS
Similar Questions
A magnetic needle has magnetic moment of 6⋅7×10−2Am2 and moment of inertial of 7⋅5×10−6kgm2. It perform 10 complete oscillations in 6⋅70s. What is the magnitude of the magnetic field?
View SolutionA magnetic needle has a magnetic moment 5.8×10−2 A m2 and moment of inertia of 7.8×10−6kg m2 , it performs 12 complete oscillations in 6.0 s. What is the magnitude of magnetic field ?
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
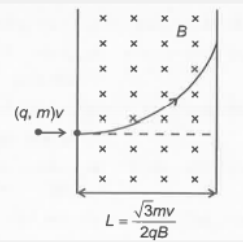 View Solution
View SolutionA magnetic needle of magnetic moment 6⋅7×10−2Am2 and moment of inertia 7⋅5×10−6kgm2 is performing simple harmonic oscillations in a magnetic field of 0⋅01T. Time taken for 10 complete oscillation is
View SolutionA magnetic dipole of magnetic moment 6×10−2Am2 and moment of inertia 12×10−6kgm2 performs oscillations in a magnetic field of 2×10−2 T. The time taken by the dipole to complete 20 oscillations is (π≈3)
View SolutionThe magnetic moment of a magnet is 0.25A−m2 . It is suspended in a magnetic field of intesity 2×10−5 T . The couple acting on it when deflected by 30∘ from the magnetic fields is .
View SolutionTwo identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View SolutionA magnetic wire of dipole moment 4πAm2 is bent in the form of semicircle. The new magnetic moment is
View SolutionA proton enter in a uniform magnetic field of 2.0 mT at an angle of 60degrees with the magnetic field with speed 10m/s. Find the picth of path
View SolutionThe component of the magnetic field along the line OP at due to the point P due to the bar magnet of magnetic moment 1.732Am2 is
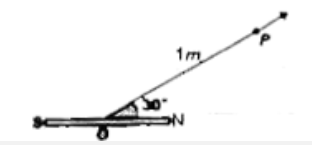 View Solution
View Solution

