Two different wire loops are concentric and lie in the same plane. The current in the outer loop is clockwise and increasing with time. The induced current in the inner loop then is
clockwise
zero
counter-clockwise
in a direction that depends on the ratio of the loop radii
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving two concentric loops, the direction of the current in the outer loop, and the resulting induced current in the inner loop.
Step 1: Understand the Setup
We have two concentric wire loops that lie in the same plane. The outer loop has a clockwise current that is increasing with time.
Hint: Remember that the direction of the current in the outer loop will affect the magnetic field it produces.
Step 2: Determine the Magnetic Field Direction
The current in the outer loop is clockwise. According to the right-hand rule, the magnetic field produced by a clockwise current will point downwards (into the plane of the loops) at the center of the loops.
Hint: Use the right-hand rule to visualize the direction of the magnetic field created by the current in the outer loop.
Step 3: Analyze the Change in Magnetic Flux
Since the current in the outer loop is increasing, the magnetic field (and thus the magnetic flux) through the inner loop is also increasing. The magnetic flux through the inner loop is given by the product of the magnetic field and the area of the inner loop.
Hint: Remember that an increasing magnetic field through a loop indicates that the magnetic flux through that loop is also increasing.
Step 4: Apply Lenz's Law
Lenz's Law states that the induced current in a loop will flow in such a direction as to oppose the change in magnetic flux through the loop. Since the magnetic flux through the inner loop is increasing in the downward direction (into the plane), the induced current must flow in a direction that creates an opposing magnetic field.
Hint: Think about how to oppose an increasing magnetic field that is directed downwards.
Step 5: Determine the Direction of Induced Current
To oppose the increase in downward magnetic flux, the induced current in the inner loop must flow in the counterclockwise direction. This counterclockwise current will create a magnetic field that points upwards (out of the plane of the loops), opposing the increase in downward magnetic flux.
Hint: Visualize the induced current and its effect on the magnetic field to confirm the direction.
Final Answer
The induced current in the inner loop is counterclockwise.
We have two concentric wire loops that lie in the same plane. The outer loop has a clockwise current that is increasing with time.
The current in the outer loop is clockwise. According to the right-hand rule, the magnetic field produced by a clockwise current will point downwards (into the plane of the loops) at the center of the loops.
Since the current in the outer loop is increasing, the magnetic field (and thus the magnetic flux) through the inner loop is also increasing. The magnetic flux through the inner loop is given by the product of the magnetic field and the area of the inner loop.
Lenz's Law states that the induced current in a loop will flow in such a direction as to oppose the change in magnetic flux through the loop. Since the magnetic flux through the inner loop is increasing in the downward direction (into the plane), the induced current must flow in a direction that creates an opposing magnetic field.
To oppose the increase in downward magnetic flux, the induced current in the inner loop must flow in the counterclockwise direction. This counterclockwise current will create a magnetic field that points upwards (out of the plane of the loops), opposing the increase in downward magnetic flux.
The induced current in the inner loop is counterclockwise.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
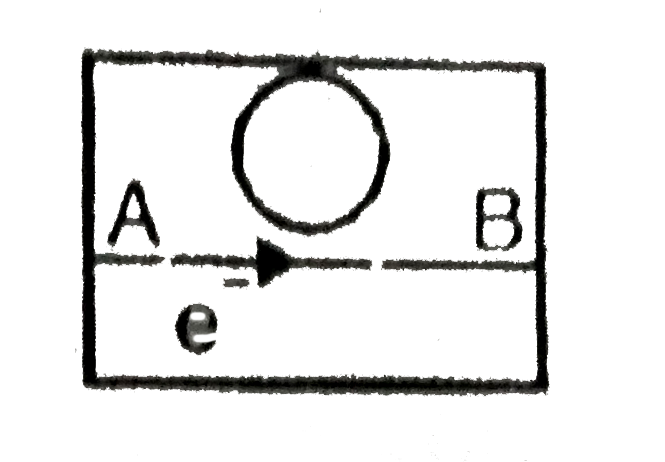
An electron is moving near to a conducting loop then the induced current in the loop is-
View SolutionAn infinite current-carrying conductor is placed along the z-axis and a wire loop is kept in the x−y plane. The current in the conductor is increasing with time. Then the
View SolutionIf the current flowing in a circular loop is in clockwise directions, then the magnetic induction will be
View SolutionIf the current in the inner loop changes according to i=2t2 then, find the current in the capacitor as a function of time.

View SolutionA small circular loop of wire of radius a is located at the centre of a much larger circular wire loop of radius b. The two loops are in the same plane. The outer loop of radius b carries an alternating current I=I0cos(ωt). The emf induced in the smaller inner loop is nearly ?
View SolutionTwo circular loops lie side by side in the same plane. One is connected to a source that supplies an increasing current, the other is a simple closed ring. Is the induced current in the ring is in the same direction as that in the loop connected to the source or opposite? What if the current in the first loop is decreasing?
View SolutionAn electron moves along the line XOX' which lies in the same plane as the square loop of conducting wire as shown. The direction of induced current, if any in the loop is
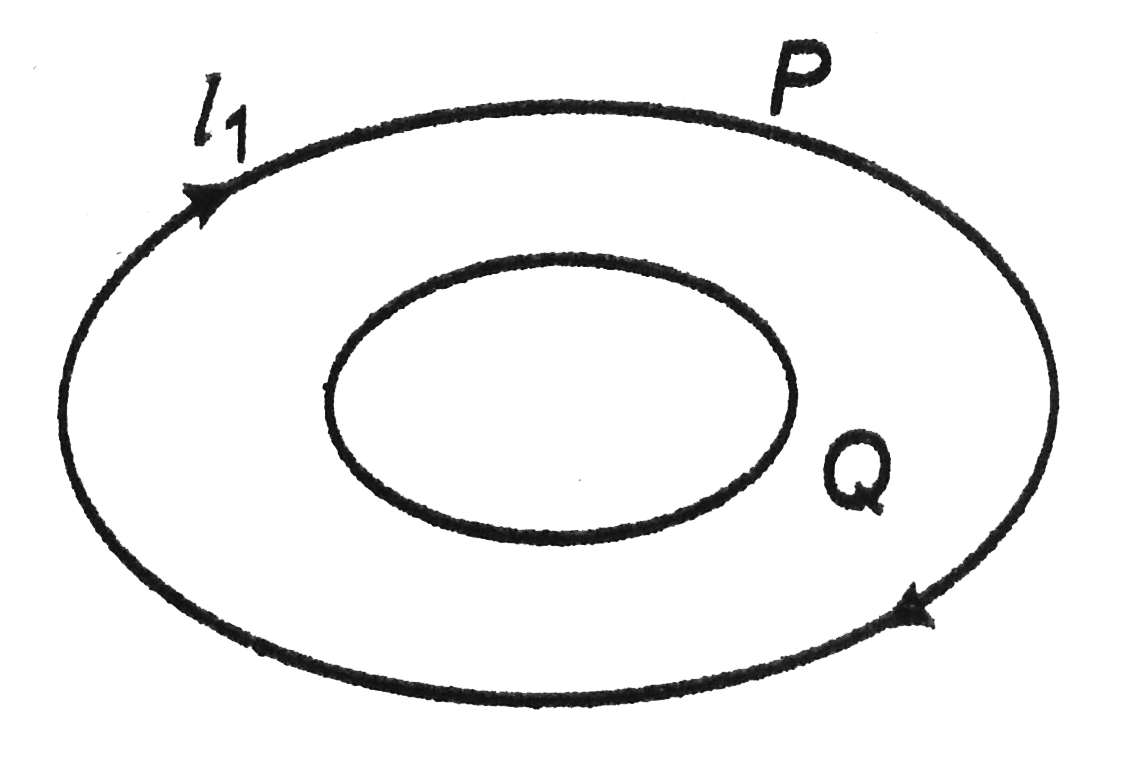
View SolutionTwo circular loops P and Q are concentric and coplanar as shown in figure. The loop Q is smaller than. P. If the current I1 flowing i loop P is decreasing with time, then the curren I2 in the loop Q
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View SolutionIf the current in the inner loop changes according to I=2t2 (Fig .), then find the current in the capacitor as a function of time.

View Solution