An infinitely long cylinder is kept parallel to an uniform magnetic field B directed along positive z-axis. The direction of induced current as seen from the z-axis will be
clockwise of the positive Z-axis
anti positive Z-axis clockwise of the positive z-axis
zero
along the magnetic field
The correct Answer is:C
To determine the direction of the induced current in an infinitely long cylinder kept parallel to a uniform magnetic field directed along the positive z-axis, we can follow these steps:
1. Understanding the Setup:
- We have an infinitely long cylinder placed parallel to a uniform magnetic field B that is directed along the positive z-axis.
2. Magnetic Flux Calculation:
- The magnetic flux Φ through the cylinder is given by the formula:
Φ=B⋅A=BAcosθ
- Here, θ is the angle between the magnetic field B and the area vector A of the surface of the cylinder. Since the cylinder is parallel to the magnetic field, θ=90∘.
3. Evaluating the Flux:
- Since cos90∘=0, the magnetic flux through the cylinder becomes:
Φ=BA⋅0=0
- This indicates that there is no magnetic flux through the cylinder.
4. Induced EMF and Current:
- According to Faraday's law of electromagnetic induction, the induced electromotive force (emf) E is given by:
E=−dΦdt
- Since Φ=0, it follows that:
dΦdt=0⟹E=0
- If the induced emf is zero, then the induced current I in the circuit is also zero, as given by Ohm's law:
I=ER=0R=0
5. Conclusion:
- Since there is no induced current in the cylinder due to the absence of changing magnetic flux, the direction of the induced current as seen from the z-axis is none. Therefore, the correct answer is that there is no induced current.
- We have an infinitely long cylinder placed parallel to a uniform magnetic field B that is directed along the positive z-axis.
- The magnetic flux Φ through the cylinder is given by the formula:
Φ=B⋅A=BAcosθ
- Here, θ is the angle between the magnetic field B and the area vector A of the surface of the cylinder. Since the cylinder is parallel to the magnetic field, θ=90∘.
- Since cos90∘=0, the magnetic flux through the cylinder becomes:
Φ=BA⋅0=0
- This indicates that there is no magnetic flux through the cylinder.
- According to Faraday's law of electromagnetic induction, the induced electromotive force (emf) E is given by:
E=−dΦdt
- Since Φ=0, it follows that:
dΦdt=0⟹E=0
- If the induced emf is zero, then the induced current I in the circuit is also zero, as given by Ohm's law:
I=ER=0R=0
- Since there is no induced current in the cylinder due to the absence of changing magnetic flux, the direction of the induced current as seen from the z-axis is none. Therefore, the correct answer is that there is no induced current.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Identify the direction of induced current as seen from the above in the following cases.
(a)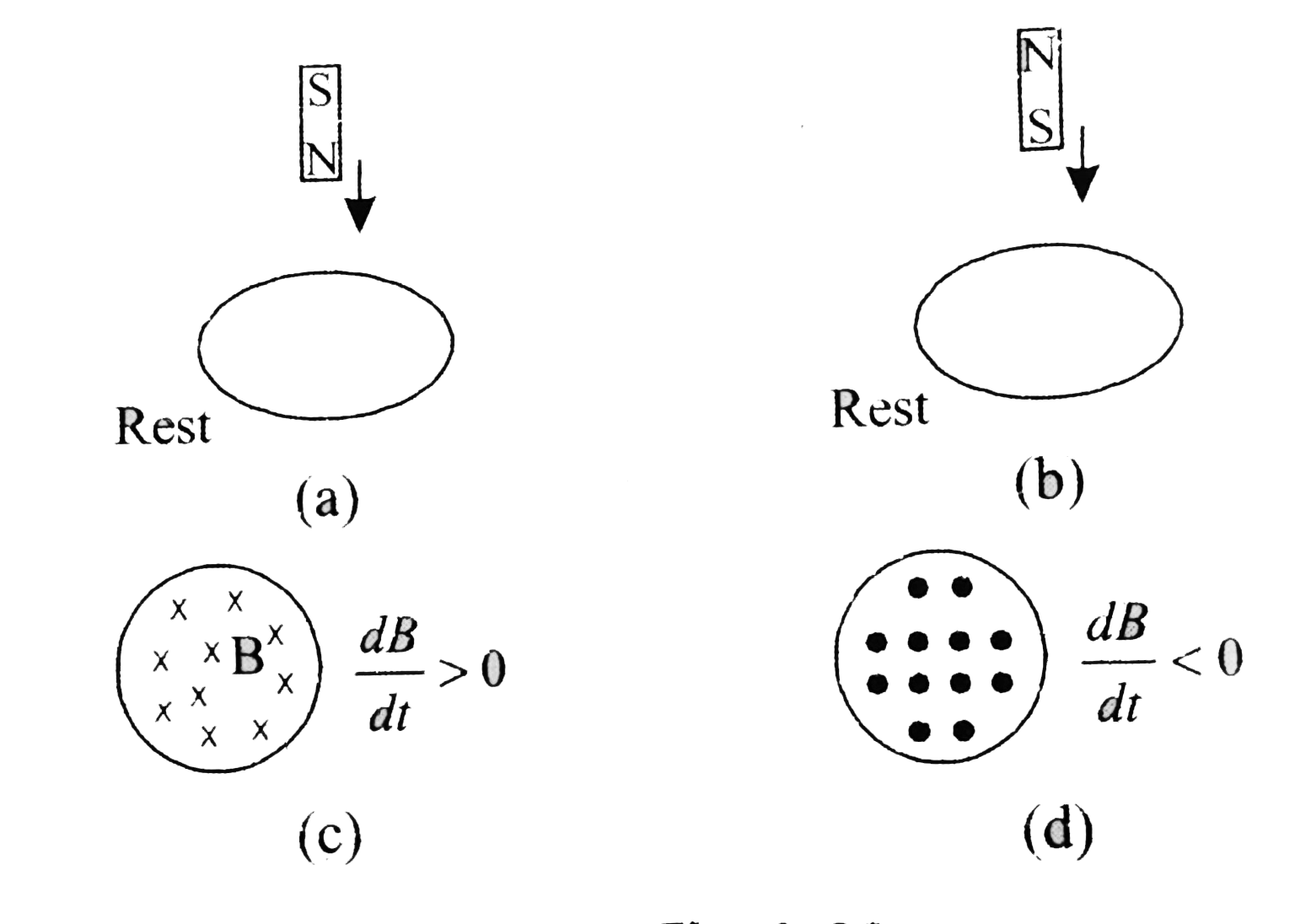 View Solution
View SolutionA conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
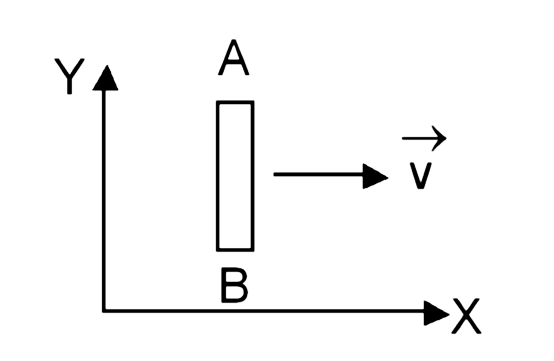 View Solution
View SolutionWrite the direction cosines of a line parallel to z-axis.
View SolutionConsider the following figure, a uniform magnetic field of 0.2 T is directed along the positive X-axis. The magnetic flux through top surface of the figure.
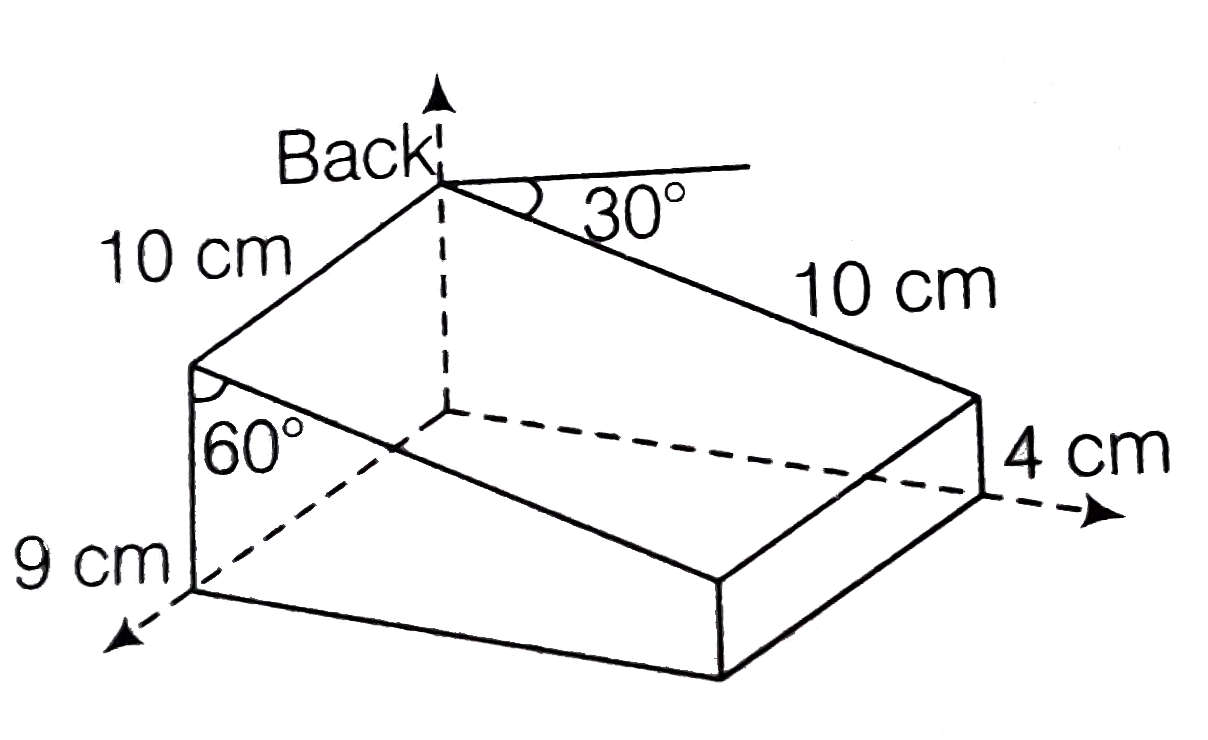 View Solution
View SolutionAn electron is projected along positive z-axis, magnetic field is present along y-axis then direction of initial acceleration of the particle is
View SolutionA rectangular, a square , a circular and an elliptical loop, all in the (x−y) plane, are moving out of a uniform magnetic field with a constant velocity →v=vˆi . The magnetic field is directed along the negative z-axis direction. The induced emf, during the passage of these loops , out of the field region, will not remain constant for :
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
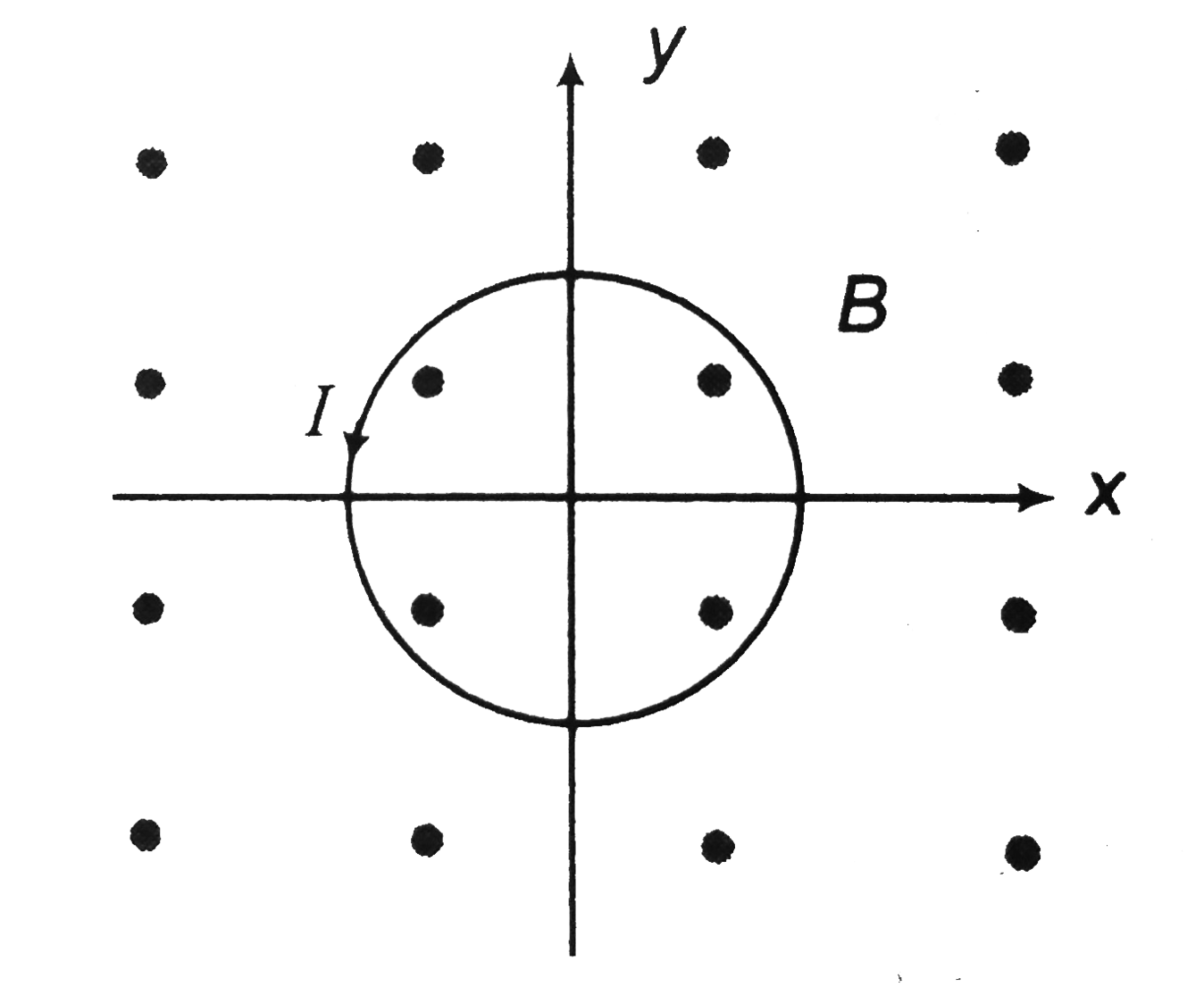 View Solution
View SolutionA conducting loop is moving from left to right through a region of uniform magnetic (B) field. Its four positiors are shown belwo. Show the direction of induced current in all four positions.
 View Solution
View Solution

