A direct current of 2 A and an alternating current having a maximum value of 2 A flow through two identical resistances. The ratio of heat produced in the two resistances will be
0.042361111111111
0.043055555555556
2
0.16736111111111
The correct Answer is:C
To solve the problem of finding the ratio of heat produced in two identical resistances when a direct current (DC) and an alternating current (AC) flow through them, we can follow these steps:
Step 1: Understand the heat produced by DC
The heat produced in a resistor due to a direct current can be calculated using Joule's law, which states that the heat (H) produced is given by:
H=I2Rt
where:
- I is the current,
- R is the resistance,
- t is the time for which the current flows.
For the DC circuit, we have:
- I=2A
Thus, the heat produced in the DC circuit (let's call it H1) is:
H1=(2)2Rt=4Rt
Step 2: Understand the heat produced by AC
For the alternating current, we need to consider the root mean square (RMS) value of the current. The RMS value of an AC current is given by:
Irms=Imax√2
where Imax is the maximum (peak) value of the AC current.
Given:
- Imax=2A
Thus, the RMS value of the AC current is:
Irms=2√2=√2A
Now, we can calculate the heat produced in the AC circuit (let's call it H2):
H2=I2rmsRt=(√2)2Rt=2Rt
Step 3: Calculate the ratio of heat produced
Now, we need to find the ratio of heat produced in the two resistances:
Ratio=H1H2=4Rt2Rt
The R and t terms cancel out:
Ratio=42=2
Conclusion
The ratio of heat produced in the two resistances is:
Ratio=2:1
The heat produced in a resistor due to a direct current can be calculated using Joule's law, which states that the heat (H) produced is given by:
H=I2Rt
where:
- I is the current,
- R is the resistance,
- t is the time for which the current flows.
- I=2A
H1=(2)2Rt=4Rt
For the alternating current, we need to consider the root mean square (RMS) value of the current. The RMS value of an AC current is given by:
Irms=Imax√2
where Imax is the maximum (peak) value of the AC current.
- Imax=2A
Irms=2√2=√2A
H2=I2rmsRt=(√2)2Rt=2Rt
Now, we need to find the ratio of heat produced in the two resistances:
Ratio=H1H2=4Rt2Rt
Ratio=42=2
The ratio of heat produced in the two resistances is:
Ratio=2:1
Similar Questions
A steady current of magnitude I and an AC current of peak value I are allowed to pass through identical resistors for the same time. The ratio of heat produced in the two resistors will be
View SolutionA direct current of 10 A is superimposed on an alternating current / = 40 cos ωt (A) flowing through a wire. The effective value of the resulting current will be
View SolutionA direct current of 5 amp is superimposed on an alternating current I=10sinωt flowing through a wire. The effective value of the resulting current will be:
View SolutionA direct current of 5 amp is superimposed on an alternating current I=10sinωt flowing through a wire. The effective value of the resulting current will be:
View SolutionThe current flowing in 3Ω Resistance will be
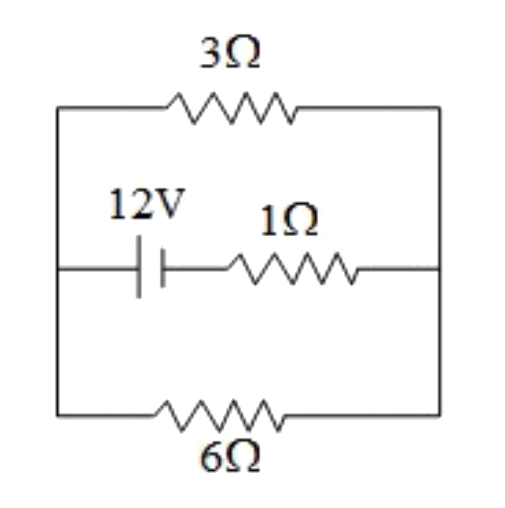
View SolutionA capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionIf a direct current of value a ampere is superimposed on an alternating current1=bsinωt flowing through a wire, what is the effective value of the resulting current in the circuit?
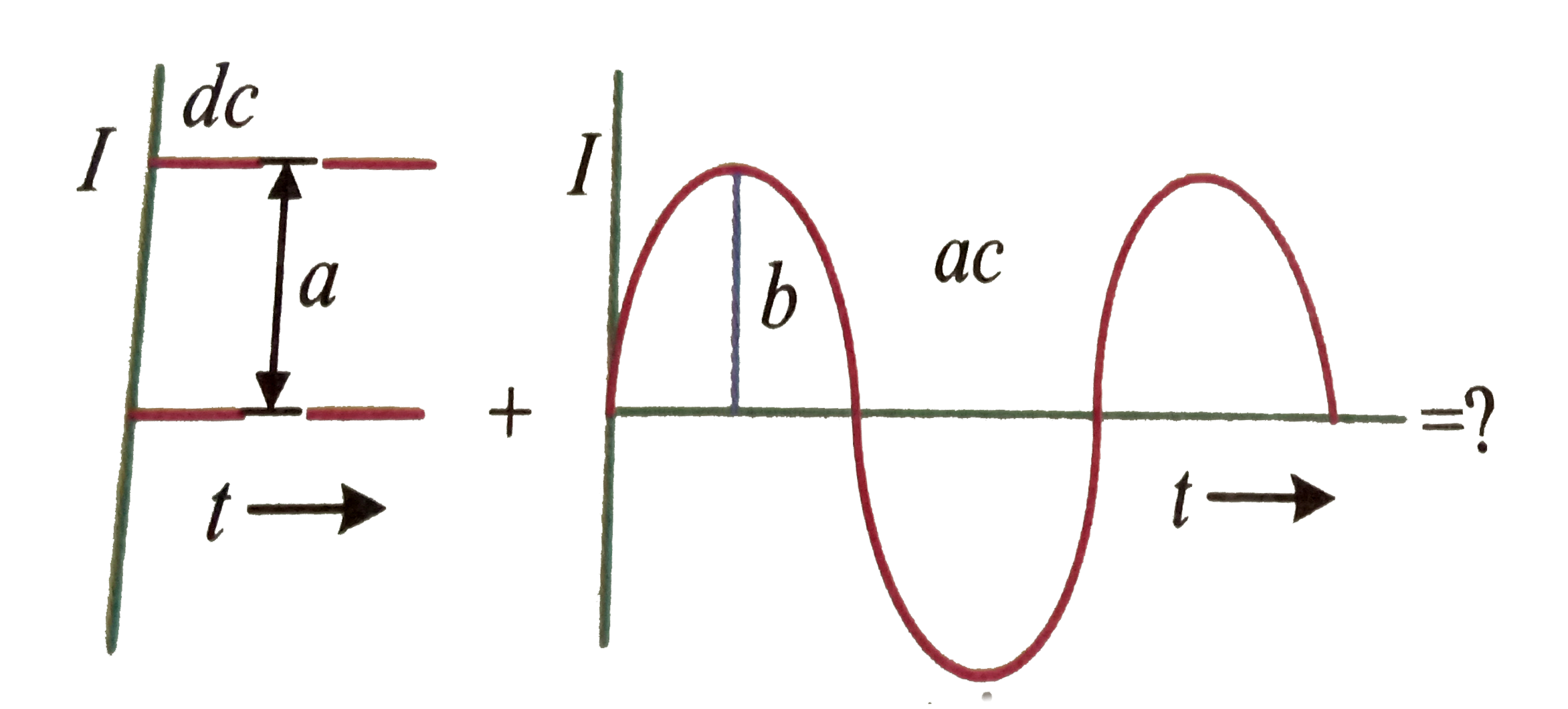
View SolutionIn a heating arrangement , an alternating current having a peak value of 28 A is used . To produce the same heat energy , If the constant current is used, its magnitude must be
View SolutionIf a direct current of value a ampere is superimposed on an alternative current I=b sinωt flowing through a wire, what is the effective value of the resulting current in the circuit?

View Solution
