One face of a prism with a refrective angle of 30∘ is coated with silver. A ray of light incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. What is the refractive index of the prism?
√2
3/√2
1.5
1.33
The correct Answer is:A
To find the refractive index of the prism, we will follow these steps:
Step 1: Understand the Geometry of the Prism
The prism has a refracting angle (A) of 30∘. A ray of light is incident on one face of the prism at an angle of 45∘. The ray is refracted into the prism and then reflects off the silver-coated face, retracing its path.
Step 2: Identify the Angles
Let:
- A=30∘ (the refracting angle of the prism)
- i=45∘ (the angle of incidence on the first face)
- R1 = angle of refraction at the first face.
Step 3: Apply the Geometry of the Situation
Since the ray retraces its path after reflecting from the silver-coated face, we can use the geometry of the situation:
- The sum of angles in the triangle formed by the angles at the prism's vertex is 180∘:
90∘−R1+90∘+A=180∘
Substituting A=30∘:
90∘−R1+90∘+30∘=180∘
This simplifies to:
180∘−R1+30∘=180∘
Thus,
R1=30∘
Step 4: Use Snell's Law
Now we apply Snell's Law at the first interface:
n1sin(i)=n2sin(R1)
Where:
- n1=1 (refractive index of air)
- n2=μ (refractive index of the prism)
- i=45∘
- R1=30∘
Substituting the values:
1⋅sin(45∘)=μ⋅sin(30∘)
Using known values:
sin(45∘)=1√2,sin(30∘)=12
Thus:
1√2=μ⋅12
Step 5: Solve for the Refractive Index
Rearranging the equation gives:
μ=2√2=√2
Final Answer
The refractive index of the prism is μ=√2.
---
The prism has a refracting angle (A) of 30∘. A ray of light is incident on one face of the prism at an angle of 45∘. The ray is refracted into the prism and then reflects off the silver-coated face, retracing its path.
Let:
- A=30∘ (the refracting angle of the prism)
- i=45∘ (the angle of incidence on the first face)
- R1 = angle of refraction at the first face.
Since the ray retraces its path after reflecting from the silver-coated face, we can use the geometry of the situation:
- The sum of angles in the triangle formed by the angles at the prism's vertex is 180∘:
90∘−R1+90∘+A=180∘
Substituting A=30∘:
90∘−R1+90∘+30∘=180∘
This simplifies to:
180∘−R1+30∘=180∘
Thus,
R1=30∘
Now we apply Snell's Law at the first interface:
n1sin(i)=n2sin(R1)
Where:
- n1=1 (refractive index of air)
- n2=μ (refractive index of the prism)
- i=45∘
- R1=30∘
1⋅sin(45∘)=μ⋅sin(30∘)
Using known values:
sin(45∘)=1√2,sin(30∘)=12
Thus:
1√2=μ⋅12
Rearranging the equation gives:
μ=2√2=√2
The refractive index of the prism is μ=√2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question23videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.710videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
A prism ABC of angle 30∘ has its face AC silvered. A ray of light incident at an angle of 45∘ at the face AB retraces its path after refraction at face AB and reflection at face AC . The refractive index of the material of the prism is
 View Solution
View SolutionOne of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View SolutionA glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionA ray of light is incident on the face AB of a glass prism ABC having vertex anlge A equal to 30∘. The face AC is silvered and a ray of light incident on the face AB retraces its path. If the refractive index of the material of prism is √3 find the angle of incidence on the face AB.
View SolutionAn isosceles prism of angle A=30∘ has one of its surfaces silvered. Light rays falling at an angle of incidence 60∘ on the other surface retrace their path after reflection from the silvered surface. The refractive index of prism material is
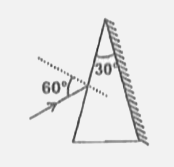 View Solution
View SolutionAngle of a prism is 30∘ and its refractive index is √2 and one of the surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path ?
View Solution

