Angle of prism is A and its one surface is silvered. Light rays falling at an angle of incidence 2A on first surface return back through the same path after suffering reflection at second silvered surface. Refraction index of the material of prism is
2sinA
2cosA
12cosA
tan A
The correct Answer is:B
To find the refractive index of the material of the prism when one surface is silvered, we can follow these steps:
1. Understanding the Setup:
- We have a prism with an angle A.
- One surface of the prism is silvered (reflective).
- A light ray is incident on the first surface at an angle of incidence 2A.
2. Refraction at the First Surface:
- When the light ray strikes the first surface of the prism, it undergoes refraction.
- Let the angle of refraction be r.
- According to Snell's law, we have:
sin(2A)=μsin(r)
- Here, μ is the refractive index of the prism.
3. Geometry of the Prism:
- The internal angles of the prism can be analyzed. The angle of the prism is A, and the angles at the interface can be expressed as:
A+(90∘−r)+90∘=180∘
- Simplifying this gives:
A+90∘−r+90∘=180∘⟹A+180∘−r=180∘⟹r=A
4. Substituting the Angle of Refraction:
- Now substituting r=A back into Snell's law:
sin(2A)=μsin(A)
5. Expressing the Refractive Index:
- Rearranging the equation gives:
μ=sin(2A)sin(A)
- Using the double angle identity for sine, we have:
sin(2A)=2sin(A)cos(A)
- Therefore, substituting this into the equation for μ:
μ=2sin(A)cos(A)sin(A)
- The sin(A) terms cancel out:
μ=2cos(A)
6. Final Result:
- The refractive index of the material of the prism is:
μ=2cos(A)
- We have a prism with an angle A.
- One surface of the prism is silvered (reflective).
- A light ray is incident on the first surface at an angle of incidence 2A.
- When the light ray strikes the first surface of the prism, it undergoes refraction.
- Let the angle of refraction be r.
- According to Snell's law, we have:
sin(2A)=μsin(r)
- Here, μ is the refractive index of the prism.
- The internal angles of the prism can be analyzed. The angle of the prism is A, and the angles at the interface can be expressed as:
A+(90∘−r)+90∘=180∘
- Simplifying this gives:
A+90∘−r+90∘=180∘⟹A+180∘−r=180∘⟹r=A
- Now substituting r=A back into Snell's law:
sin(2A)=μsin(A)
- Rearranging the equation gives:
μ=sin(2A)sin(A)
- Using the double angle identity for sine, we have:
sin(2A)=2sin(A)cos(A)
- Therefore, substituting this into the equation for μ:
μ=2sin(A)cos(A)sin(A)
- The sin(A) terms cancel out:
μ=2cos(A)
- The refractive index of the material of the prism is:
μ=2cos(A)
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
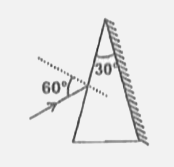
An isosceles prism of angle A=30∘ has one of its surfaces silvered. Light rays falling at an angle of incidence 60∘ on the other surface retrace their path after reflection from the silvered surface. The refractive index of prism material is
View SolutionA prism ABC of angle 30∘ has its face AC silvered. A ray of light incident at an angle of 45∘ at the face AB retraces its path after refraction at face AB and reflection at face AC . The refractive index of the material of the prism is

View SolutionAngle of a prism is 30∘ and its refractive index is √2 and one of the surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path ?
View SolutionA ray is ihncident at an angle of incidence ii on one surface of a prism of small angle A and emerge normally from opposite surface. If the refractive index of the material of prism is μ. the angel of incidance I is nearly equal to
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View SolutionA ray of light falling at an angle of 50∘ is refracted through a prism and suffers minimum deviation. The angle of the prism is 60∘. Find the angle of minimum deviation and refraction index of the material of the prism.
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionA ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
View Solution
