Question

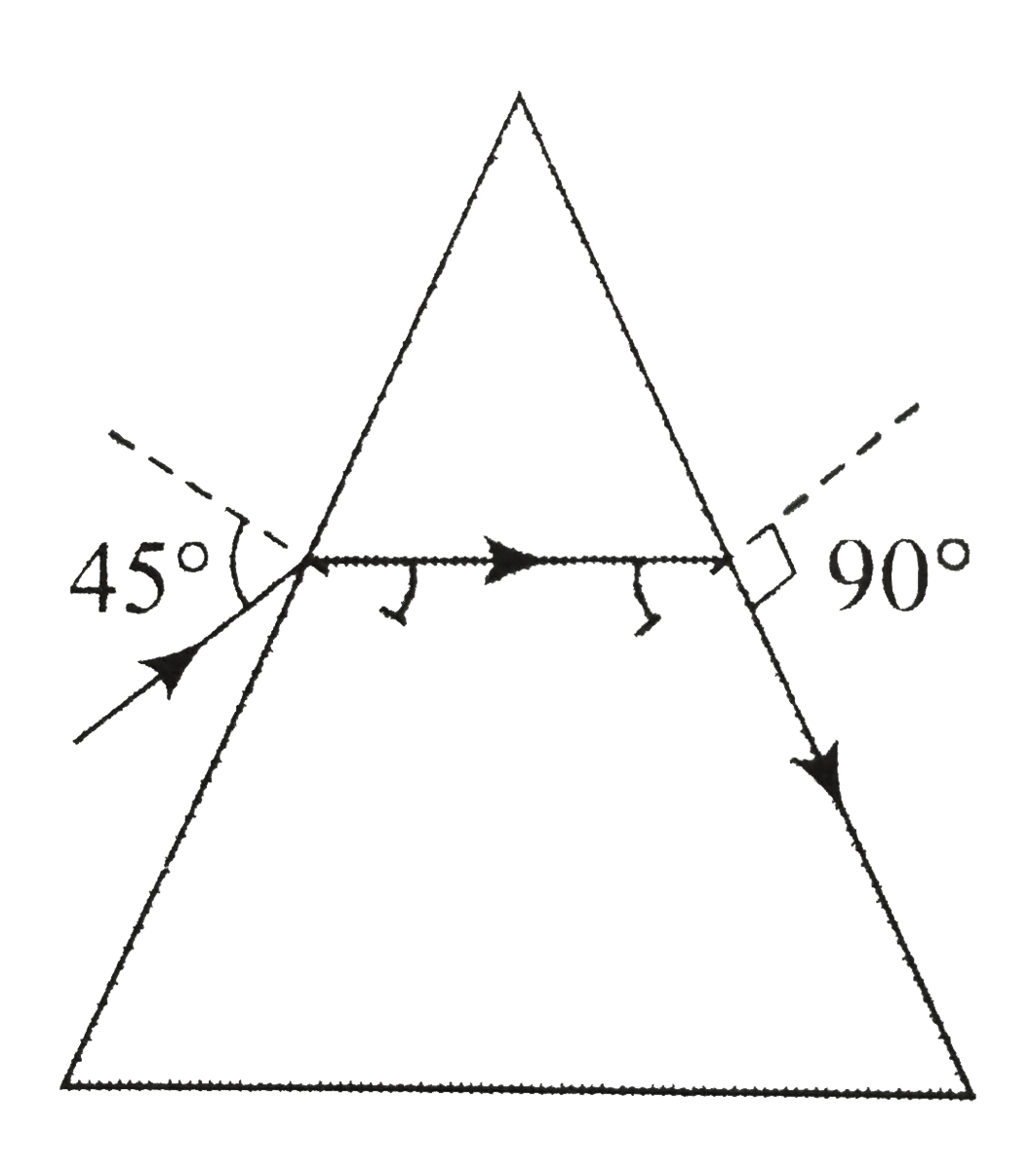
For a ray of light refracted through a prism of angle ${\displaystyle {60}^{\circ }}$, the angle of incidence is equal to the angle of emergence, each equal to ${\displaystyle {45}^{\circ }}$. Find the refractive index of the material of the prism.

Explanation

To find the refractive index of the material of a prism with an angle of 60 degrees, where the angle of incidence (I) and angle of emergence (E) are both 45 degrees, we can follow these steps:

1. Identify the Given Values:
- Angle of the prism (A) = 60 degrees
- Angle of incidence (I) = 45 degrees
- Angle of emergence (E) = 45 degrees

2. Recognize the Condition of Minimum Deviation:
- Since the angle of incidence is equal to the angle of emergence (I = E), we are dealing with the case of minimum deviation. In this case, the angles of refraction at both faces of the prism are equal (r1 = r2 = r).

3. Relate the Angles:
- For a prism, the relationship between the angle of the prism (A), angle of refraction (r), and the angles of incidence and emergence can be expressed as:
\( A = r_1 + r_2 \)
- Since \( r_1 = r_2 = r \), we can write:
\( A = 2r \)
- Therefore, we can find r:
\( r = \frac{A}{2} = \frac{60^\circ}{2} = 30^\circ \)

4. Use Snell's Law:
- Snell's Law states that:
\( n = \frac{\sin I}{\sin r} \)
- Here, \( n \) is the refractive index, \( I \) is the angle of incidence, and \( r \) is the angle of refraction.

5. Calculate the Sine Values:
- Calculate \( \sin I \) and \( \sin r \):
- \( \sin I = \sin 45^\circ = \frac{1}{\sqrt{2}} \)
- \( \sin r = \sin 30^\circ = \frac{1}{2} \)

6. Substitute into Snell's Law:
- Substitute the values into the formula for the refractive index:
\( n = \frac{\sin I}{\sin r} = \frac{\frac{1}{\sqrt{2}}}{\frac{1}{2}} = \frac{1}{\sqrt{2}} \times 2 = \frac{2}{\sqrt{2}} = \sqrt{2} \)

7. Final Answer:
- The refractive index of the material of the prism is:
\( n = \sqrt{2} \)