Young's double slit experiment is carried out using microwaves of
wavelength λ=3cm. Distance between the slits is d=5cm and the distance
between the plane of slits and the screen is D=100cm.
(a) Find total number of maxima and
(b) their positions on the screen.
To solve the problem, we will break it down into two parts: finding the total number of maxima and then determining their positions on the screen.
Part (a): Finding the Total Number of Maxima
1. Given Data:
- Wavelength, λ=3cm
- Distance between the slits, d=5cm
- Distance from the slits to the screen, D=100cm=1m
2. Formula for Maxima:
The condition for maxima in Young's double slit experiment is given by:
yn=nλDd
where yn is the position of the nth maxima, n is the order of the maxima, λ is the wavelength, D is the distance to the screen, and d is the distance between the slits.
3. Finding Maximum Order n:
The maximum order n can be found when yn is less than or equal to the distance from the central maximum to the edge of the screen. The maximum possible value of yn occurs when:
yn≤d2
Rearranging gives:
n≤d2⋅dλD
Substituting the values:
n≤52⋅53⋅100
Simplifying:
n≤5⋅52⋅3⋅100=25600=0.04167
Since n must be a whole number, the maximum possible value of n is 0.
4. Total Number of Maxima:
Since n can take values from 0 to n, the total number of maxima is:
n+1=0+1=1
Part (b): Finding the Positions of the Maxima
1. Position of the First Maxima:
The position of the first maxima can be calculated using:
y1=1⋅λDd
Substituting the values:
y1=1⋅3⋅1005=60cm
2. Position of the Other Maxima:
Since the maximum order n is 0, there are no other maxima to consider.
Final Answers:
(a) Total number of maxima = 1
(b) Position of maxima on the screen = 60 cm
- Wavelength, λ=3cm
- Distance between the slits, d=5cm
- Distance from the slits to the screen, D=100cm=1m
The condition for maxima in Young's double slit experiment is given by:
yn=nλDd
where yn is the position of the nth maxima, n is the order of the maxima, λ is the wavelength, D is the distance to the screen, and d is the distance between the slits.
The maximum order n can be found when yn is less than or equal to the distance from the central maximum to the edge of the screen. The maximum possible value of yn occurs when:
yn≤d2
Rearranging gives:
n≤d2⋅dλD
Substituting the values:
n≤52⋅53⋅100
Simplifying:
n≤5⋅52⋅3⋅100=25600=0.04167
Since n must be a whole number, the maximum possible value of n is 0.
Since n can take values from 0 to n, the total number of maxima is:
n+1=0+1=1
The position of the first maxima can be calculated using:
y1=1⋅λDd
Substituting the values:
y1=1⋅3⋅1005=60cm
Since the maximum order n is 0, there are no other maxima to consider.
(a) Total number of maxima = 1
(b) Position of maxima on the screen = 60 cm
Topper's Solved these Questions
Similar Questions
A beam of light consisting of two wavelenths, 6500 Å and 5200 Å is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen in 120 cm. (a) Find the distance of the third bright frings on the screen from the central maximum for the wavelength 6500 Å (b) What is the least distance from the central maximum where the bright frings due to both the wavlelengths coincide ?
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
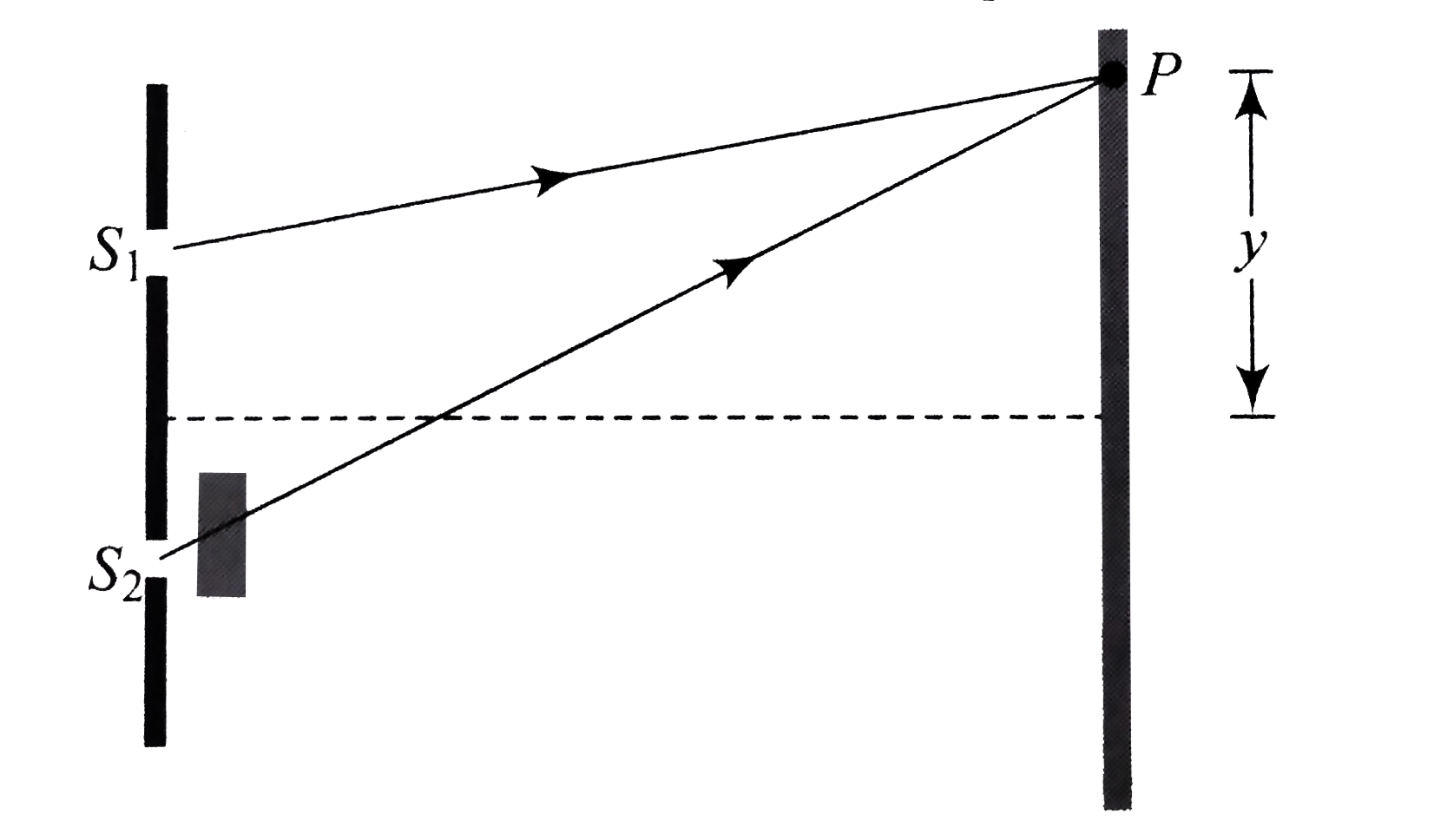
Intensity at point P is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
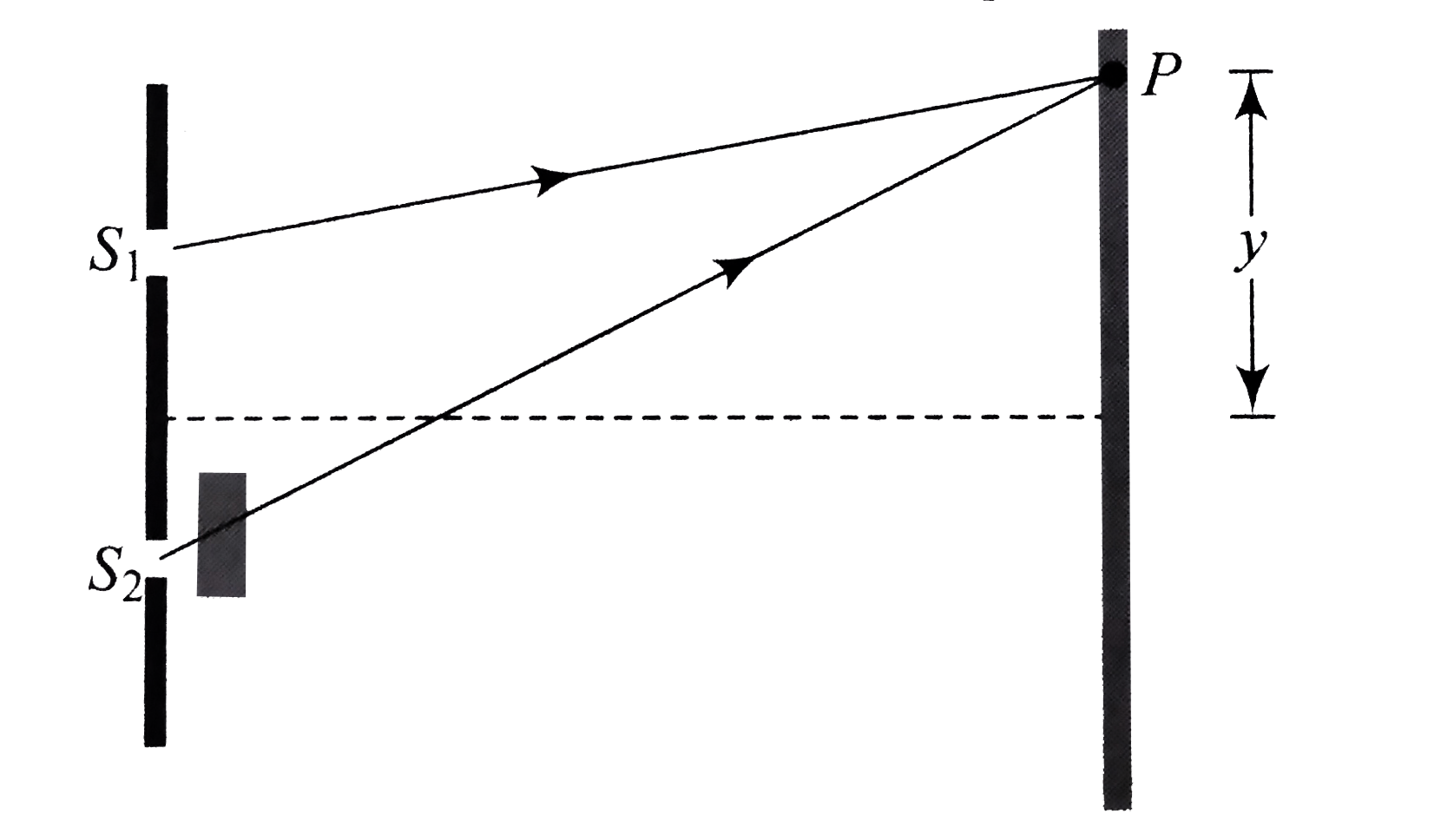
The value of η is
View SolutionThe Young's double slit experiment is carried out with light of wavelength 5000Å. The distance between the slits is 0.2mm and the screen is at 200cm from the slits. The central maximum is at y=0. The third maximum will be at y equal to
View SolutionA beam of light consisting of two wavelength , 6500A∘ and 5200A∘ is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits 2.0 mm and the distance between the plane of the slits and the screen is 120 cm. Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 6500Å.
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiement when wavelength used is 6000Å and the screen is 40cm from the slits, the fringes are 0.012cm wide. What is the distance between the slits?
View Solution
