For triangle ABC, R = 5/2 and r=1. Let I be the incenter of the triangle and D,E,andF be the feet of the perpendiculars from I to BC,CAandAB, respectively. The value of ID×IE×IFIA×IB×IC is equal toSolution in Telugu
52
54
110
15
The correct Answer is:C
Step by step video, text & image solution for For triangle ABC, R = 5/2 and r=1. Let I be the incenter of the triangle and D, E, and F be the feet of the perpendiculars from I to BC,CA and AB, respectively. The value of (IDxx IExxIF)/(IAxxIBxxIC) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (More than one correct answer Type Questions)19videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL II) (LECTURE SHEET (ADVANCED)) (Matrix Matching Type Questions)9videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE SHEET (EXERCISE-IV) (LEVEL-II) (Matrix Matching Type Questions)2videos
PROPERTIES OF TRIANGLES
- BOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS30videos
PLANES
- BOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES55videos
PROPERTIES OF VECTORS
Similar Questions
In a triangle ABC, the altitude from A is not less than BC and the altitude from B is not then less than AC. The triangle is
03:58View SolutionObserve the following Columns.
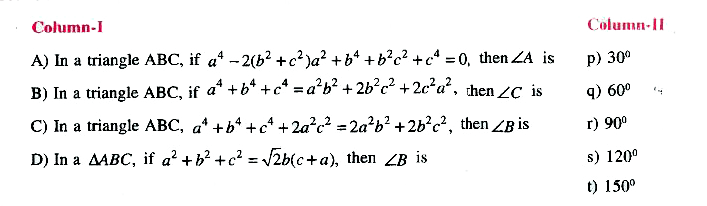 05:10View Solution
05:10View SolutionLet O be the circumcentre, H be the orthocentre, I be the incentre and I1I2,I3 be the excentres of acuteangled ΔABC
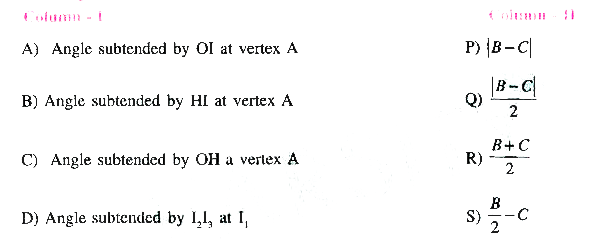 08:07View Solution
08:07View SolutionThe plane 2x + 3y + kz - 7 = 0 is parallel to the line whose d.r's are (2,-3,1) then k=
View SolutionIf ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
View SolutionFor triangle ABC,R=52andr=1. Let I be the incenter of the triangle and D,EandF be the feet of the perpendiculars from I→BC,CAandAB, respectively. The value of IDxIExIFIAxIBxIC is equal to (a) 52 (b) 54 (c) 10 (d) 15
02:40View SolutionFor a triangle ABC,R=52andr=1. Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of (IA)(IB)(IC)(ID)(IE)(IF) is equal to _____
07:58View SolutionThe midpoints of the sides BC, CA and AB of a △ABC are D(2,1), E(-5,7)and F-5, -5) respectively. Find the equations of the sides of △ABC.
05:30View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
02:06View SolutionP is a point inside a ΔABC, D, E, F are the feet or perpendicular from P to the line BC, AB respectively. Show that BCPD+CAPE+ABPF≥2s2Δ. Prove that equality holds if P is its incentre,s=semipermeter,Delta = area of triangle.
View SolutionΔABC లో AB,BC మరియు CA భుజాల మద్య బిందువులు వరుసగా D, E మరియు F లు అయిన ΔDEF:ΔABC =
View SolutionFor triangle ABC,R=52andr=1. Let I be the incenter of the triangle and D,EandF be the feet of the perpendiculars from I→BC,CAandAB, respectively. The value of ID⋅IE⋅IFIA⋅IB⋅IC is equal to (a) 52 (b) 54 (c) 110 (d) 15
04:17View SolutionLet ABC be a triangle with incentre I and inradius r. Let D, E, F be the feet of the perpendiculars from I to the sides BC, CA and AB, respectively, If r2 and r3 are the radii of circles inscribed in the quadrilaterls AFIE, BDIF and CEID respectively, then prove that r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
10:40View SolutionFor a triangle ABC,R=52andr=1. Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of (IA)(IB)(IC)(ID)(IE)(IF) is equal to _____
05:16View SolutionIn a ΔABC,BC=2,CA=1+√3 and ∠C=60∘. Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.
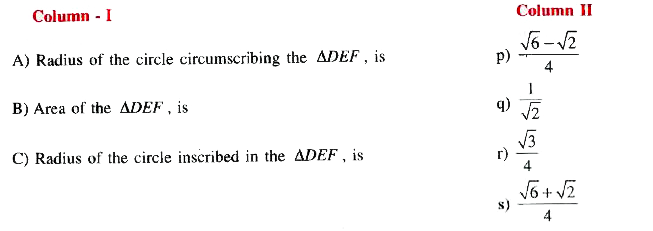 04:30View Solution
04:30View Solution

