sin−1t√1+t2 का cos−11√1+t2 का सापेक्ष अकवल गुणांक है :
1∀t>0
−1∀t<0
1∀t∈R
इनमे से कोई नहीं
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
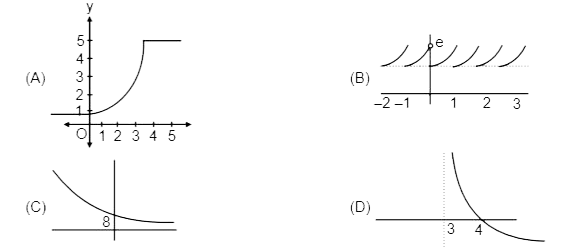
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
View Solutionif x=sqrt((1-t^(2))/(1+t^(2))),y=(sqrt(1+t^(2))-sqrt(1-t^(2)))/(sqrt(1+t^(2))+sqrt(1-t^(2))) then (dy)/(dx)
View SolutionThe expression (1)/(sqrt(2)){(sin tan^(-1)cos tan^(-1)t)/(cos tan^(-1)sin cot^(-1)sqrt(2)t)}*{sqrt((1+2t^(2))/(2+t^(2)))}
View SolutionDerivative of sin−1(t√1+t2) with respect to cos−1(1√1+t2 is
View SolutionIf x=sin−1(t√1+t2),y=cos−1(1√1+t2),show that dydx=1
View Solutiondydx ज्ञात कीजिए -
x=sin−1.t√1+t2,y=cos−1.1√1+t2
View SolutionDerivative of cos−1[1√t2+1w.r.tsin−1[t√t2+1] is
View SolutionIf cosx=1√1+t2, and siny=t√1+t2, then dydx =
View Solutionयदि cosx=1√1+t2 और siny=t√1+t2तो सिध्द कीजिए कि dydx=1
View Solutionx=cos−1(1√1+t2),y=sin−1(t√1+t2)⇒dydx is equal to
View Solution(1−t61−t)3 के प्रसार में t4 का गुणांक है
View SolutionIf cos x =1/sqrt(1+t^(2)) , and sin y = t/sqrt(1+t^(2)) , then (dy)/(dx) =
View SolutionIf x=cos^-1(1/(sqrt(1+t^2))) , y=sin^-1(1/(sqrt(t^2+1))) then dy/dx is independent of t.
View SolutionIf x=√1−t21+t2,y=√1+t2−√1−t2√1+t2+√1−t2 then dydx =
View Solution
