यदि सभी n∈N के लिए fn(x)=efn−1(x) f _(0) (x) =xऔर{f _(n) (x)}हैतो,ddx{fnx))} का मान है -
fn(x).ddx(fn−1(x)}
fn(x).fn−1(x)
fn(x)(x).Fn−1(x)………f2(x).F1(x)
इनमे से कोई नहीं
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
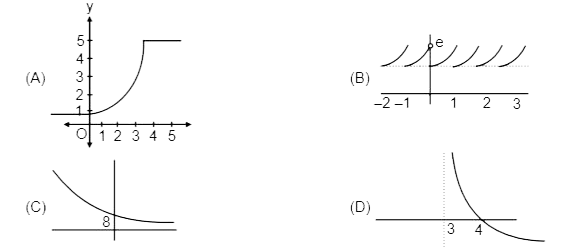
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
View SolutionIf f(x)=xn where x∈R , then differentiation of xn with respect to x isxn−1.
View SolutionEvaluate ∫f(x) is polynomaial function of then the degree, prove that ∫exf(x)dx=ex[f(x)f'(x)+fx=fx+......+(−1)nfn(x)] where fn(x)dx+dnfdxn
View Solutionf(x)=(2x-pi)^(3)+2x-cos x,Th e n,(d)/(dx)[f^(-1)(x)] at x=pi is equal to :
View Solution(i)If f(x)=xn; where n ε R then the differentiation of xn with respect to x is nxn−1
View SolutionUsing mathematical induction prove that : ddx(xn)=nxn−1 for all n∈N.
View SolutionLet f1(x)=exandfn+1(x)=efn(x)) for any n≥1,n∈N.Then for any fixed n, the vlaue of ddxf)(n)(x) equals:
View Solutionयदि धनात्मक पूर्णक n के लिए f(n)=sinnθ+cosnθ है तो f(3)−f(5)f(5)−f(7) का मान है |
View Solutionयदि वास्तविक मान फलन f(x)=ax−1xn(ax+1) सम है, तब n का मान है
View SolutionStatement 1: If differentiable function f(x) satisfies the relation f(x)+f(x−2)=0∀x∈R, and if (ddxf(x))x=a=b,then(ddxf(x))x=a+4000=b. Statement 2: f(x) is a periodic function with period 4.
View SolutionIf f(x) is polynomaial function of degree n, prove that ∫exf(x)dx=ex[f(x)−f'(x)+f''(x)−f'''(x)+......+(−1)nfn(x)] where fn(x)=dnfdxn
View SolutionIf f(x)andg(x) are two differentiable functions, show that f(x)g(x) is also differentiable such that ddx[f(x)g(x)]=f(x)ddx{g(x)}+g(x)ddx{f(x)}
View SolutionIf f(x)=xnwheren∈R, then differentiation of xn with respect to xsinxn−1.
View SolutionIf f(x)andg(x) a re differentiate functions, then show that f(x)±g(x) are also differentiable such that ddx{f(x)±g(x)}=ddx{f(x)}±ddx{g(x)}
View Solution
