$\to a and - - \to - a$ are collinear (true or false)Solution in Malayalam

Video Solution

Text Solution

Verified by Experts

1

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

THREE DIMENSTIONAL GEOMETRYBOOK - A N EXCEL PUBLICATIONCHAPTER - THREE DIMENSTIONAL GEOMETRYEXERCISE - QUESTION BANK
97 Videos

Similar Questions

Consider the points A(0,0,2) and B(3,0,1) . Write direction ratio of the joining A and B.
View Solution
Supposing Newton's law of gravitation for gravitation force $F_{1}$ and $F_{2}$ between two masses $m_{1}$ and $m_{2}$ at positions $r_{1}$ and $r_{2}$ read $F_{2} = - F_{2} = \frac{r_{12}}{r_{12}^{3}} G M_{0}^{2} {(\frac{m_{1} m_{2}}{M_{0}^{2}})}^{n}$ where $M_{0}$ is a constant dimension of mass, $r_{12} = r_{1} - r_{2}$ and $n$ is number. In such a case.
View Solution
A charged particle can be deflected by electric and magnetic filed both The electric force ${\to F}_{e} = q \to E$ and magnetic force $- \to F_{m} = \to q v \times \to B q$ = charge in coulomb, oversetrarrV is velocity in m//s $\to E$ is electric filed strengh in $N / C$ and $B$ is magnetic field strength in tesla $(T)$ If a moving charged particle enters simultaneous electric and magnetic field, the net force on the charged particle is
$\to F = q (\to E + \to v \times \to B)$
If $\to F = 0$ the charged particle will move undeflected in simultaneous fields
A charged particle moves in simultaneous electric field $\to E$ and magnetic field $\to B$ If the charged particle passes undeflected , then the value of electric field vectore $\to E$ must be .
View Solution
A charged particle can be deflected by electric and magnetic filed both The electric force oversetrarrF_(e) =qoversetrarrE and magnetic force oversetrarr(F_(m)) = oversetrarr(qv)xxoversetrarr(B) q = charge in coulomb, oversetrarrV is velocity in m/s oversetrarrE is electric filed strengh in N//C and B is magnetic field strength in tesla (T) If a moving charged particle enters simultaneous electric and magnetic field, the net force on the charged particle is oversetrarr(F) =q(oversetrarrE +oversetrarr(v) xx oversetrarrB) If oversetrarr(F) =0 the charged particle will move undeflected in simultaneous fields If electric field is along Y axis and charged particle moves along X axis the magnetic field must be .
View Solution
A charged particle can be deflected by electric and magnetic filed both The electric force oversetrarrF_(e) =qoversetrarrE and magnetic force oversetrarr(F_(m)) = oversetrarr(qv)xxoversetrarr(B) q = charge in coulomb, oversetrarrV is velocity in m/s oversetrarrE is electric filed strengh in N//C and B is magnetic field strength in tesla (T) If a moving charged particle enters simultaneous electric and magnetic field, the net force on the charged particle is oversetrarr(F) =q(oversetrarrE +oversetrarr(v) xx oversetrarrB) If oversetrarr(F) =0 the charged particle will move undeflected in simultaneous fields If a charged particle moving along x-axis enters the simultaneous electric and magnetic fields at right angles Electric field is along y-axis and magnetic field along z-axis and vgt(E)/(B) the particle will .
View Solution
Satement -1: A beam of electron passes undeflected through region $\to E & \to B$
In the region $\to E & \to B$ are present and perpendicular to each other and the particle is moving perpendicular to both of them .
Statement-2: In the region $\to E & \to B$ , both are present and perpendicular to each other and the particle is moving perpendicular to both of them.
View Solution
PQRS is a parallelogram and oversetrarr(QS) and oversetrarr(PR) are its diagonals .Show that vec(PR)+ vec(QS)-2vec(QR)=0
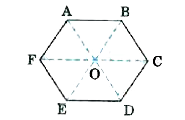
View Solution
For a regular hexagon ABCDEF shown below , prove that
$- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = 6 - - \to A O .$

View Solution
Can we beam oversetrarr(OA) Ray of oversetrarr(AO) Can write Why? Or why not?
View Solution
Given co-ordinates of the points A and B as $(- 1, - 2)$ and $(- 5, - 6)$ respectively, what is the magnitude of $- - \to A B$ ?
View Solution
Find the direction cosines of the vectors, $\to r_{1} - \to r_{2}$ whaere $\to r_{1} = ˆ i + ˆ j + ˆ k$ and $\to r_{2} = 2 ˆ i + ˆ j + 2 ˆ k$ .
View Solution
Write the direction ratios of the vector $\to a = \land i + \land 2 j - \land k$ and calculate its direction cosines ?
View Solution
Suppose ABC is a triangle and D and E are the mid points of AB and AC respectively.
Choose the correct answer from the bracket and fill in the blank
$- - \to B A + - - \to A C = \dots \dots$
(oversetrarr(CB),oversetrarr(BC),1/2 oversetrarrr(BC),2oversetrarr(BC))
View Solution
Suppose a and b represent in magnitude and direction the two sides AB and BC of the regular hexagon ABCDEF as shown in the figure.Find $- - \to C D, - - \to D E, - - \to E F and - - \to F A$ in terms of $\to a$ "and"oversetrarrb
View Solution
The position vectors of the points A,B,C are given to be $\land i + 2 \land j + 3 \land k, 4 \land i + 4 \land k and - 2 \land k$ respectively.
Find $- - \to A B and - - \to A C$
View Solution

A N EXCEL PUBLICATION-VECTOR ALGEBRA-QUESTION BANK

Home
Ask Doubt
Profile