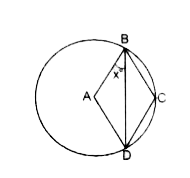
In the figure given above, A is the centre of the circle and AB = BC = CD. What is the value of x ?
20∘
2212∘
25∘
30∘
The correct Answer is:D
Step by step video & image solution for In the figure given above, A is the centre of the circle and AB = BC = CD. What is the value of x ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
In the figure given above AO=CD where
O is the centre of the circle. What is ∠APB equal to ?View SolutionIn the figure (i) given below, O is the centre of the circle. AB and CD are the chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB=24 cm OM=5 cm, ON=12 cm. Find the, (i) radius of the circle (ii) length of chord CD (ii) In the figure (ii) given below, CD is diameter which meets the chord AB at E such that AE = BE = 4 cm.If CE = 3 cm, find the radius of the circle.
View Solution
Knowledge Check
- Question 1 - Select One
In the figure given above AO=CD where
O is the centre of the circle. What is ∠APB equal to ?A60∘B50∘C45∘D30∘ - Question 2 - Select One
In the given figure, O is the centre of the circle. The value of x is
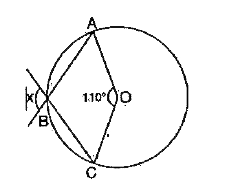A75∘B55∘C125∘D110∘ - Question 3 - Select One
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘
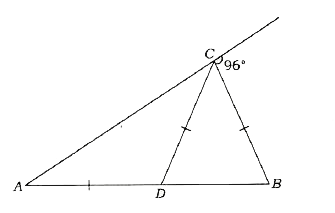
In the figure given above, AD = CD = BC. What is the value of ∠CDB?View Solution
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.View SolutionIn the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).
View Solution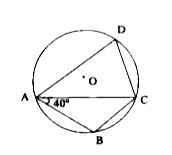
In the figure given above, O is the centre of a circle circumscribing a quadrilateral ABCD. If AB=BC and ∠BAC=40∘, then what is ∠ADC equal to ?View Solution-
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.View Solution