Two tangents PA and PB are drawn from a point P to the circle. If the radius of the circle is 5 cm and AB = 6 cm and O is the centre of the circle. OP cuts AB at C and OC = 4 cm, then OP :-
254 cm
25 cm
13 cm
None of these
The correct Answer is:A
To solve the problem, we need to find the length of OP given the radius of the circle, the length of the tangent segment AB, and the length OC. Here are the steps to find OP:
Step 1: Understand the Geometry
We have a circle with center O and radius 5 cm. Two tangents PA and PB are drawn from point P to points A and B on the circle. The length of the tangent segment AB is given as 6 cm. The line OP intersects AB at point C, and OC is given as 4 cm.
Step 2: Identify the Right Triangles
Since PA and PB are tangents to the circle, we know that OA and OB are perpendicular to the tangents at points A and B, respectively. Thus, triangles OAP and OBP are right triangles.
Step 3: Use the Pythagorean Theorem
In triangle OAP, we can apply the Pythagorean theorem:
- OA (radius) = 5 cm
- AC (half of AB) = 6 cm / 2 = 3 cm
- OP is the hypotenuse we need to find.
Using the Pythagorean theorem:
OP2=OA2+AC2
OP2=52+32
OP2=25+9
OP2=34
OP=√34
Step 4: Calculate the Length of OP
Now we can calculate the value of OP:
OP=√34≈5.83 cm
Final Answer
Thus, the length of OP is approximately 5.83 cm.
---
We have a circle with center O and radius 5 cm. Two tangents PA and PB are drawn from point P to points A and B on the circle. The length of the tangent segment AB is given as 6 cm. The line OP intersects AB at point C, and OC is given as 4 cm.
Since PA and PB are tangents to the circle, we know that OA and OB are perpendicular to the tangents at points A and B, respectively. Thus, triangles OAP and OBP are right triangles.
In triangle OAP, we can apply the Pythagorean theorem:
- OA (radius) = 5 cm
- AC (half of AB) = 6 cm / 2 = 3 cm
- OP is the hypotenuse we need to find.
OP2=OA2+AC2
OP2=52+32
OP2=25+9
OP2=34
OP=√34
Now we can calculate the value of OP:
OP=√34≈5.83 cm
Thus, the length of OP is approximately 5.83 cm.
Topper's Solved these Questions
Similar Questions
In the tangent of the circle. A tangent PT is drawn from an out side point P to the circle. If radius of circle is 5 cm and OP=13 cm then find the length of tangent PT.
 View Solution
View SolutionA tangent is drawn from an external point O to a circle of radius 3 units at P such that OP = 4 units. If C is the centre of the circle, then the sine of the angle COP is
View Solution
Knowledge Check
- Question 1 - Select One
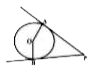
PA and PB are tangents to the circle and O is the centre of the circle . The radius is 5 cm and PO is 13 cm . Find the area PBOAAa) √1213Bb) 2413Cc) √2413Dd) 60 - Question 2 - Select One
In the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
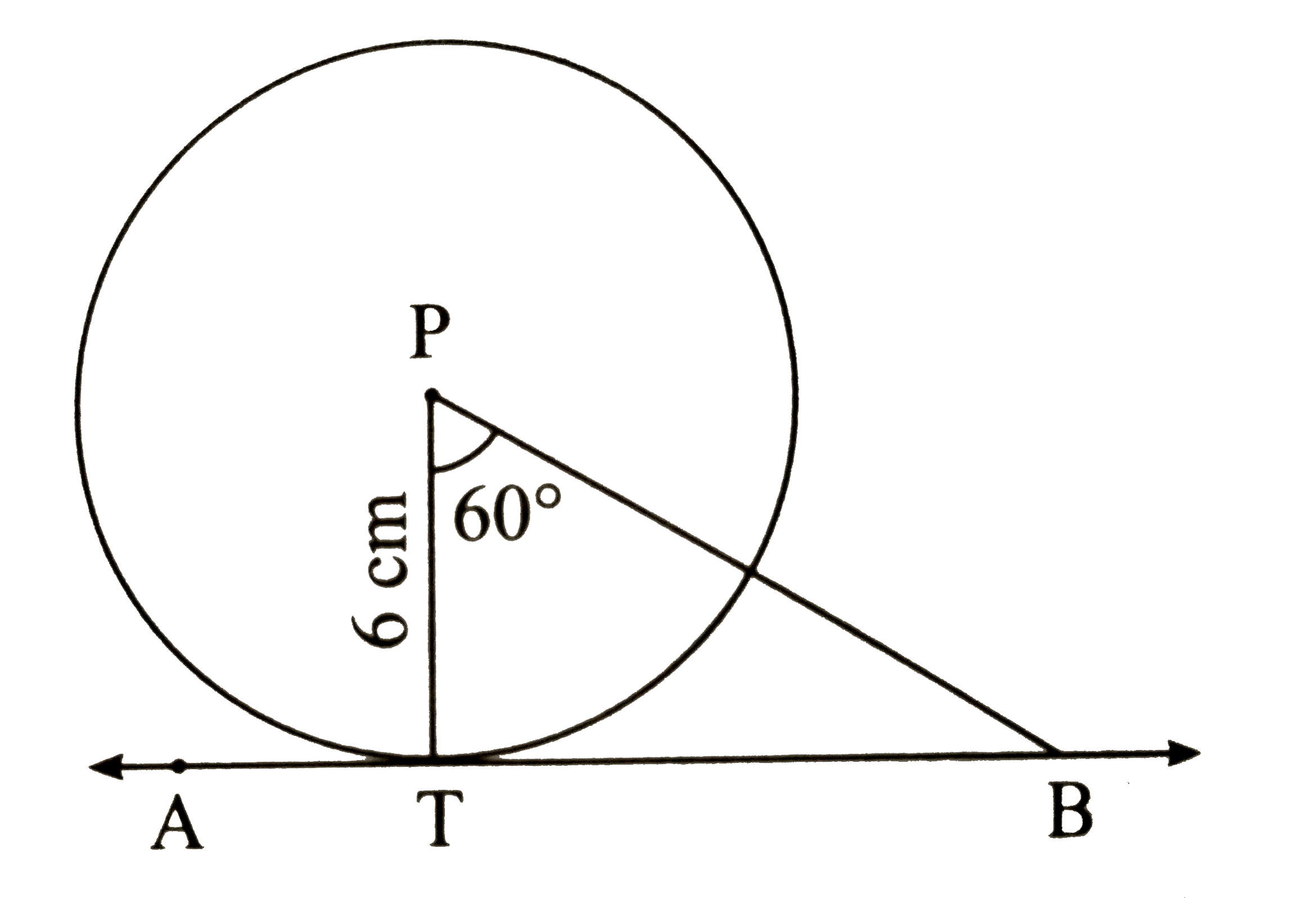 A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cm
A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cm - Question 3 - Select One
In the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
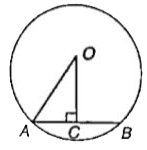 A35 cmB30 cmC15 cmD18 cm
A35 cmB30 cmC15 cmD18 cm
O is the centre of the circle. OP = 5 and OT = 4, and AB = 8. The line PT is a tangent to the circle. Find PB
 View Solution
View SolutionIn the adjoining figure, PA and PB are tangents from P to a circle with center C.If the radius of the circle is 4 cm and PA perpendicular PB.Find the length of the tangent.
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.
 View Solution
View SolutionIn the given figure, OP=13 cm, AB=7 cm and BP=9 cm. Find the radius of the circle.
 View Solution
View SolutionThe length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
View Solution

