Two concentric circles with centre P have radii 6.5 cm and 3.3 cm. Through a point A of the larger circle, a tangent is drawn to the smaller circle touching it at B and the larger circle at C. find the length of the tangent
5.6 cm
11.2 cm
11.8 cm
6.5 cm
The correct Answer is:B
To find the length of the tangent drawn from point A on the larger circle to the smaller circle, we can follow these steps:
1. Identify the Given Information:
- Radius of the larger circle (R) = 6.5 cm
- Radius of the smaller circle (r) = 3.3 cm
- Let point A be on the circumference of the larger circle, and point B be the point where the tangent touches the smaller circle.
2. Draw the Diagram:
- Draw two concentric circles with center P.
- Mark point A on the circumference of the larger circle.
- Draw a tangent line from point A that touches the smaller circle at point B.
3. Understand the Geometry:
- The line segment PB (from the center P to point B) is the radius of the smaller circle and is perpendicular to the tangent line AC at point B.
- The line segment PA (from the center P to point A) is the radius of the larger circle.
4. Apply the Pythagorean Theorem:
- In triangle PAB, we can apply the Pythagorean theorem:
PA2=PB2+AB2
- Here, PA is the hypotenuse, PB is one leg, and AB is the other leg.
5. Substitute the Known Values:
- Substitute the values of PA and PB:
(6.5)2=(3.3)2+AB2
6. Calculate the Squares:
- Calculate PA2 and PB2:
6.52=42.25
3.32=10.89
7. Set Up the Equation:
- Substitute the squared values into the equation:
42.25=10.89+AB2
8. Solve for AB^2:
- Rearranging gives:
AB2=42.25−10.89=31.36
9. Take the Square Root:
- Find AB by taking the square root:
AB=√31.36=5.6 cm
10. Calculate the Length of the Tangent AC:
- Since AC is twice the length of AB (because PB bisects AC):
AC=2×AB=2×5.6=11.2 cm
Final Answer:
The length of the tangent AC is 11.2 cm.
- Radius of the larger circle (R) = 6.5 cm
- Radius of the smaller circle (r) = 3.3 cm
- Let point A be on the circumference of the larger circle, and point B be the point where the tangent touches the smaller circle.
- Draw two concentric circles with center P.
- Mark point A on the circumference of the larger circle.
- Draw a tangent line from point A that touches the smaller circle at point B.
- The line segment PB (from the center P to point B) is the radius of the smaller circle and is perpendicular to the tangent line AC at point B.
- The line segment PA (from the center P to point A) is the radius of the larger circle.
- In triangle PAB, we can apply the Pythagorean theorem:
PA2=PB2+AB2
- Here, PA is the hypotenuse, PB is one leg, and AB is the other leg.
- Substitute the values of PA and PB:
(6.5)2=(3.3)2+AB2
- Calculate PA2 and PB2:
6.52=42.25
3.32=10.89
- Substitute the squared values into the equation:
42.25=10.89+AB2
- Rearranging gives:
AB2=42.25−10.89=31.36
- Find AB by taking the square root:
AB=√31.36=5.6 cm
- Since AC is twice the length of AB (because PB bisects AC):
AC=2×AB=2×5.6=11.2 cm
The length of the tangent AC is 11.2 cm.
Topper's Solved these Questions
Similar Questions
Two concentric circles are of radii 6.5cm and 2.5cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5cm and 3cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
View Solution
Knowledge Check
In two concentric circles of radii 15 cm and 9 cm , then length of a biggest chord of the larger circle which is a tangent to the smaller circle is .
A24cmB20 cmC12 cmD10 cmThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmTwo concentric circles are of radius 15 cm and 9 cm. What is the length of the chord of the larger circle which is tangent to the smaller circle?
त्रिज्या 15 सेमी तथा 9 सेमी वाले दो संकेंद्री वृत्त हैं | बड़े वृत्त की जीवा की लंबाई कितनी होगी जो छोटे वृत्त पर स्पर्श रेखा है ?A5 cmB8 cmC10 cmD25 cm
Two concentric circle of radii 13cm and 12 cm. What is the length of the chord of the larger circle which is tangent to the smaller circle?
View SolutionTwo concentric circle with centre O are of radii 6 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circle as shown in the figure. If AP = 10 cm. Find BP
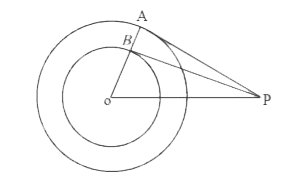
View SolutionTwo concentric circles have their radii as a and b(a>b) . PQ is the diameter of the larger circle. From Q. a tangent is drawn to smaller circle which touches it at R. length of PR is
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionTwo concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।
View Solution
