PR is a tangent at a point Q on a circle, in which Q is the centre and its radius is 8 cm. If OR = 16 cm and OP = 10 cm, then the length of PR is-
18 cm
19 cm
19.8 cm
21.86 cm
The correct Answer is:C
To solve the problem, we need to find the length of the tangent PR to the circle at point Q, given the following information:
- The radius of the circle (OQ) = 8 cm
- The distance from the center to point R (OR) = 16 cm
- The distance from point O to point P (OP) = 10 cm
1. Identify the Right Triangle OPQ:
- In triangle OPQ, O is the center of the circle, P is a point outside the circle, and Q is the point of tangency.
- OQ is the radius (8 cm), and OP is the distance from O to P (10 cm).
2. Apply the Pythagorean Theorem in Triangle OPQ:
- According to the Pythagorean theorem, we have:
OP2=OQ2+PQ2
- Substituting the known values:
102=82+PQ2
100=64+PQ2
- Rearranging gives:
PQ2=100−64=36
- Taking the square root:
PQ=√36=6 cm
3. Identify the Right Triangle OQR:
- In triangle OQR, O is the center of the circle, Q is the point of tangency, and R is a point outside the circle.
- OR is the distance from O to R (16 cm).
4. Apply the Pythagorean Theorem in Triangle OQR:
- Again, using the Pythagorean theorem:
OR2=OQ2+QR2
- Substituting the known values:
162=82+QR2
256=64+QR2
- Rearranging gives:
QR2=256−64=192
- Taking the square root:
QR=√192=8√3 cm
5. Calculate the Length of PR:
- The length of the tangent PR can be found by adding the lengths of PQ and QR:
PR=PQ+QR=6+8√3
6. Approximate the Value:
- Using √3≈1.732:
QR≈8×1.732=13.856 cm
- Therefore:
PR≈6+13.856=19.856 cm
Final Answer:
The length of PR is approximately 19.856 cm.
- The distance from the center to point R (OR) = 16 cm
- The distance from point O to point P (OP) = 10 cm
- In triangle OPQ, O is the center of the circle, P is a point outside the circle, and Q is the point of tangency.
- OQ is the radius (8 cm), and OP is the distance from O to P (10 cm).
- According to the Pythagorean theorem, we have:
OP2=OQ2+PQ2
- Substituting the known values:
102=82+PQ2
100=64+PQ2
- Rearranging gives:
PQ2=100−64=36
- Taking the square root:
PQ=√36=6 cm
- In triangle OQR, O is the center of the circle, Q is the point of tangency, and R is a point outside the circle.
- OR is the distance from O to R (16 cm).
- Again, using the Pythagorean theorem:
OR2=OQ2+QR2
- Substituting the known values:
162=82+QR2
256=64+QR2
- Rearranging gives:
QR2=256−64=192
- Taking the square root:
QR=√192=8√3 cm
- The length of the tangent PR can be found by adding the lengths of PQ and QR:
PR=PQ+QR=6+8√3
- Using √3≈1.732:
QR≈8×1.732=13.856 cm
- Therefore:
PR≈6+13.856=19.856 cm
The length of PR is approximately 19.856 cm.
Topper's Solved these Questions
Similar Questions
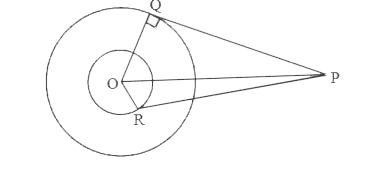
In the given figure, PQ is tangent to outer circle and PR is tangent to inner circle. If PQ = 4cm, OQ = 3 cm and OR = 2 cm then find the length of PR.
 View Solution
View SolutionIn the figure , PQ and PR are tangents drawn from and external point P to the circle with centre O. Q and R are the points of contact. If PQ = 5 cm then what is the length of segment PR ? Why ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
PR is tangent to a circle, with centre O and radius 4 cm, at point Q. If ∠POR=90∘,OR=5cmand OP=203cm, then (in cm) the length of PR :
A3B163C233D253 - Question 2 - Select One
PT is a tangent to a circle with centre O and radius 6cm. If PT is 8cm then length of OP is:
A10 cm.B12 cm.C16 cm.D9 cm. - Question 3 - Select One
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cm
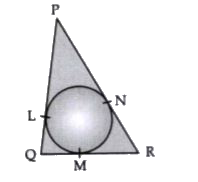
In fig , a circle isinscribed in a triangle PQR with PQ = 10 cm , QR = 8 cm and PR = 12 cm .Find the length of the QM , RN and PL.
 View Solution
View SolutionFind the length of the tangent to a circle with centre O and radius 6cm from a point P such that OP=10cm?
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionTangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
View Solution

