ABCD is a square. M is the mid-point of AB and N is the mid-point of BC. DM and AN are joined and they meet at O, then which of the following is correct ?
OA : OM = 1 : 2
AN = MD
∠ADM=∠ANB
∠AMD=∠BAN
The correct Answer is:B
To solve the problem, we need to analyze the square ABCD and the midpoints M and N, then determine the relationship between the segments AN and DM.
1. Understanding the Square and Midpoints:
- Let the vertices of the square ABCD be A(0, 0), B(1, 0), C(1, 1), and D(0, 1).
- The midpoint M of AB is calculated as:
M=(0+12,0+02)=(12,0)
- The midpoint N of BC is calculated as:
N=(1+12,0+12)=(1,12)
2. Finding the Equations of Lines DM and AN:
- Line DM:
- The slope of line DM (from D to M) is:
slope of DM=0−112−0=−112=−2
- The equation of line DM using point D(0, 1):
y−1=−2(x−0)⟹y=−2x+1
- Line AN:
- The slope of line AN (from A to N) is:
slope of AN=12−01−0=12
- The equation of line AN using point A(0, 0):
y−0=12(x−0)⟹y=12x
3. Finding the Intersection Point O:
- To find the intersection point O, set the equations of lines DM and AN equal to each other:
−2x+1=12x
- Rearranging gives:
−2x−12x=−1⟹−52x=−1⟹x=25
- Substitute x=25 back into the equation of line AN to find y:
y=12⋅25=15
- Thus, the coordinates of point O are:
O(25,15)
4. Finding Lengths AN and DM:
- Length of AN:
- Using the distance formula:
AN=√(1−0)2+(12−0)2=√1+14=√54=√52
- Length of DM:
- Using the distance formula:
DM=√(12−0)2+(0−1)2=√(12)2+(−1)2=√14+1=√54=√52
5. Conclusion:
- Since AN=DM, we conclude that:
AN=DM
- Therefore, the correct option is that AN is equal to DM.
- Let the vertices of the square ABCD be A(0, 0), B(1, 0), C(1, 1), and D(0, 1).
- The midpoint M of AB is calculated as:
M=(0+12,0+02)=(12,0)
- The midpoint N of BC is calculated as:
N=(1+12,0+12)=(1,12)
- Line DM:
- The slope of line DM (from D to M) is:
slope of DM=0−112−0=−112=−2
- The equation of line DM using point D(0, 1):
y−1=−2(x−0)⟹y=−2x+1
- The slope of line AN (from A to N) is:
slope of AN=12−01−0=12
- The equation of line AN using point A(0, 0):
y−0=12(x−0)⟹y=12x
- To find the intersection point O, set the equations of lines DM and AN equal to each other:
−2x+1=12x
- Rearranging gives:
−2x−12x=−1⟹−52x=−1⟹x=25
- Substitute x=25 back into the equation of line AN to find y:
y=12⋅25=15
- Thus, the coordinates of point O are:
O(25,15)
- Length of AN:
- Using the distance formula:
AN=√(1−0)2+(12−0)2=√1+14=√54=√52
- Using the distance formula:
DM=√(12−0)2+(0−1)2=√(12)2+(−1)2=√14+1=√54=√52
- Since AN=DM, we conclude that:
AN=DM
- Therefore, the correct option is that AN is equal to DM.
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE48videos
QUADRILATERAL
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions200videos
PROFIT & LOSS
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS113videos
RATIO & PROPORTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a square, X is the mid point of AB and Y is the mid point of BC, then which of the following is NOT correct?
AThe triangles ADX and BAY are congruentB∠DXA=∠AYBC∠ADX=∠BAYDDX is not perpendicular to AY - Question 2 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2 - Question 3 - Select One
Locus of mid point of AB is
Ax2=−2yB2x2=−yCx2=−4yDx22−y21=−1
In the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
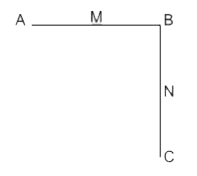 View Solution
View SolutionIn the given figure, is the mid point of BC, DE ⊥ AB and DF⊥AC such that DE= DE. Then, which of the following is true?
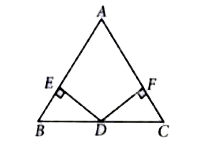 View Solution
View SolutionABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
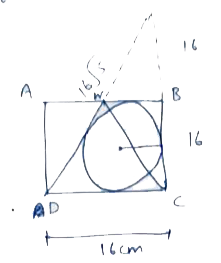 View Solution
View SolutionIf ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
View Solution

