In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AB2+BC2=CD2+DA2
AB2+CD2=BC2+DA2
AB2+AD2=BC2+CD2
AB2+BC2=2(CD2+DA2)
The correct Answer is:B
To solve the problem step by step, we will use the properties of triangles and the Pythagorean theorem.
1. Identify the Quadrilateral and Diagonals:
We have a quadrilateral ABCD with diagonals AC and BD intersecting at point M. We know that these diagonals intersect at right angles.
2. Apply Pythagorean Theorem in Triangle CDM:
In triangle CDM, we can apply the Pythagorean theorem:
CD2=DM2+CM2(Equation 1)
3. Apply Pythagorean Theorem in Triangle ADM:
In triangle ADM, we also apply the Pythagorean theorem:
AD2=AM2+DM2(Equation 2)
4. Apply Pythagorean Theorem in Triangle ABM:
In triangle ABM, we use the Pythagorean theorem:
AB2=AM2+BM2(Equation 3)
5. Apply Pythagorean Theorem in Triangle BCM:
In triangle BCM, we apply the Pythagorean theorem:
BC2=BM2+CM2(Equation 4)
6. Add All Four Equations:
Now, we add all four equations together:
(DM2+CM2)+(AM2+DM2)+(AM2+BM2)+(BM2+CM2)=CD2+AD2+AB2+BC2
This simplifies to:
2DM2+2CM2+2AM2+2BM2=CD2+AD2+AB2+BC2
7. Factor Out the Common Terms:
We can factor out the 2 from the left side:
2(DM2+CM2+AM2+BM2)=CD2+AD2+AB2+BC2
8. Divide Both Sides by 2:
Dividing both sides by 2 gives:
DM2+CM2+AM2+BM2=12(CD2+AD2+AB2+BC2)
9. Rearranging the Equation:
Rearranging the terms leads us to:
AB2+CD2=AD2+BC2
Conclusion:
Thus, we conclude that in quadrilateral ABCD, if the diagonals AC and BD intersect at right angles, then:
AB2+CD2=AD2+BC2
We have a quadrilateral ABCD with diagonals AC and BD intersecting at point M. We know that these diagonals intersect at right angles.
In triangle CDM, we can apply the Pythagorean theorem:
CD2=DM2+CM2(Equation 1)
In triangle ADM, we also apply the Pythagorean theorem:
AD2=AM2+DM2(Equation 2)
In triangle ABM, we use the Pythagorean theorem:
AB2=AM2+BM2(Equation 3)
In triangle BCM, we apply the Pythagorean theorem:
BC2=BM2+CM2(Equation 4)
Now, we add all four equations together:
(DM2+CM2)+(AM2+DM2)+(AM2+BM2)+(BM2+CM2)=CD2+AD2+AB2+BC2
2DM2+2CM2+2AM2+2BM2=CD2+AD2+AB2+BC2
We can factor out the 2 from the left side:
2(DM2+CM2+AM2+BM2)=CD2+AD2+AB2+BC2
Dividing both sides by 2 gives:
DM2+CM2+AM2+BM2=12(CD2+AD2+AB2+BC2)
Rearranging the terms leads us to:
AB2+CD2=AD2+BC2
Thus, we conclude that in quadrilateral ABCD, if the diagonals AC and BD intersect at right angles, then:
AB2+CD2=AD2+BC2
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE48videos
QUADRILATERAL
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions200videos
PROFIT & LOSS
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS113videos
RATIO & PROPORTION
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘ - Question 2 - Select One
ABCD is a quadrilateral. AM and CN are perpendiculars to BD, AM= CN and diagonals AC and BD intersect at O, then which one of the following is correct?
AAO=OCBBO=ODCAO=BODCO=DO - Question 3 - Select One
Is ||gm ABCD a square?
I. Diagonals of ||gm ABCD are equal.
II. Diagonals of ||gm ABCD intersect at right angles.Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together.
In a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn a quadrilateral ABCD it is given tghat AB∣∣CD nad the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionA cyclic quadrilateral ABCD is such that AB=BC,AD=DC and AC and BD intersect at O. If ∠CAD=46∘, then the measure of ∠AOB is equal to:
 View Solution
View SolutionIn the adjoining figure, ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB=28∘, find ∠OBC.
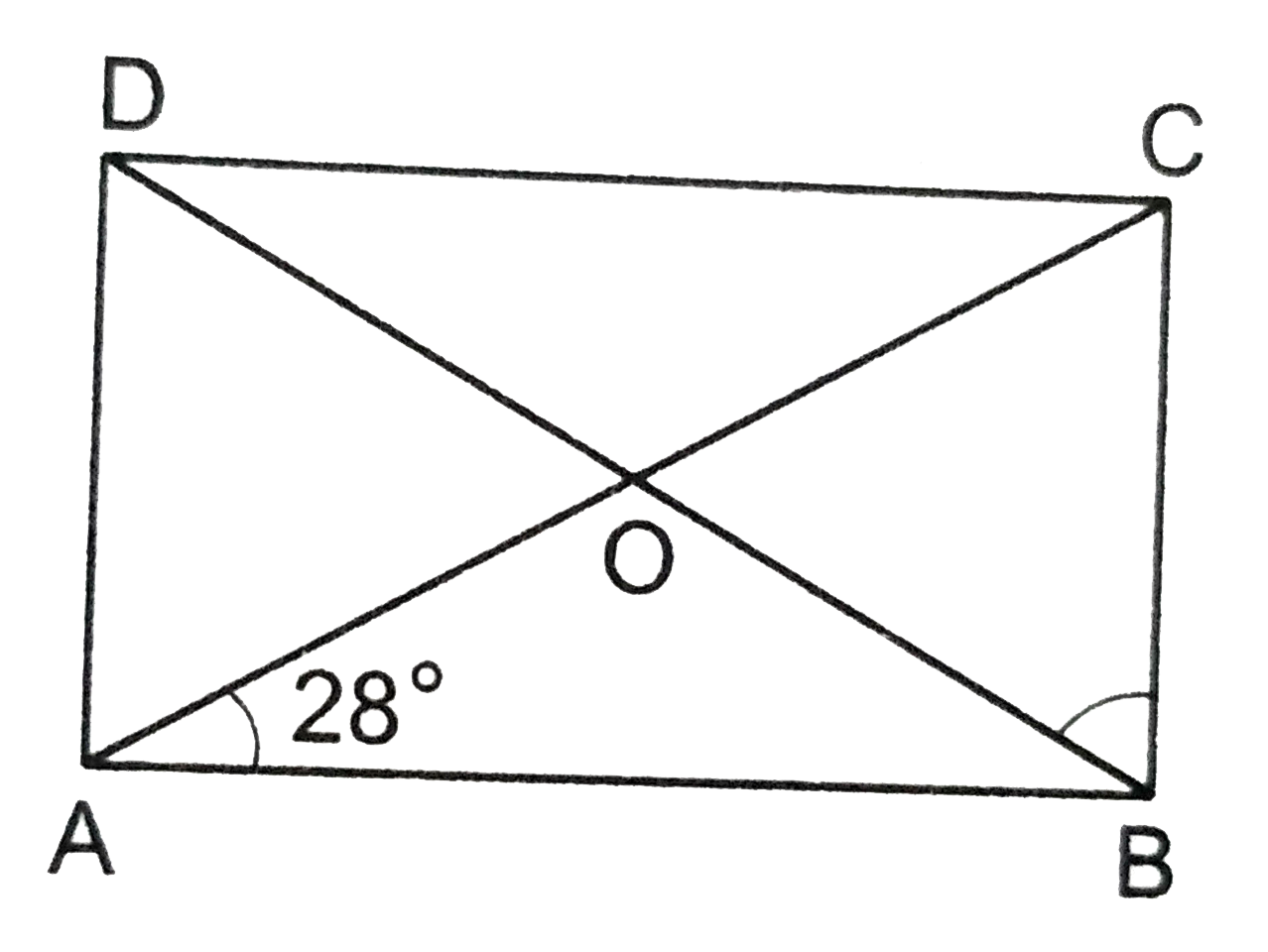 View Solution
View SolutionABCD is a quadrlateral in which BD and AC are diagonals then
View Solution


