ABCD is a quadrilateral such that ∠D=90∘. A circle C of radius r touches the sides AB, BC, CD and DA at P, Q, R and S respectively. If BC = 38 cm, CD = 25 cm and BP = 27 cm. Find r
The correct Answer is:B
To solve the problem, we need to find the radius r of the circle that touches all four sides of the quadrilateral ABCD with ∠D=90∘. Given the lengths BC=38cm, CD=25cm, and BP=27cm, we can follow these steps:
1. Identify the Tangent Segments:
Since the circle touches the sides of the quadrilateral at points P,Q,R, and S, we know that the lengths of the tangent segments from a point to a circle are equal. Therefore, we can denote:
- BP=BQ=27cm
- Let CQ=CR (we will find this value).
- Let RD=RS (we will find this value).
2. Calculate CQ:
We know that:
BC=BP+CQ
Substituting the known values:
38=27+CQ
Solving for CQ:
CQ=38−27=11cm
Thus, CQ=CR=11cm.
3. Calculate RD:
We know that:
CD=CR+RD
Substituting the known values:
25=11+RD
Solving for RD:
RD=25−11=14cm
4. Identify the Relationship in Quadrilateral:
In quadrilateral OSRD (where O is the center of the circle), we have:
- OS=OR=r (the radius of the circle).
- RD=14cm.
5. Recognize the Right Triangle:
Since ∠D=90∘, triangle OSD is a right triangle with:
- OS as one leg,
- RD as the other leg,
- OD as the hypotenuse.
6. Establish the Square:
Since OS=OR and RD is perpendicular to OS, quadrilateral OSRD forms a square. Therefore, all sides are equal:
OS=RD=14cm
7. Conclusion:
Thus, the radius r of the circle is:
r=14cm
Final Answer:
The radius r of the circle is 14cm.
Since the circle touches the sides of the quadrilateral at points P,Q,R, and S, we know that the lengths of the tangent segments from a point to a circle are equal. Therefore, we can denote:
- BP=BQ=27cm
- Let CQ=CR (we will find this value).
- Let RD=RS (we will find this value).
We know that:
BC=BP+CQ
Substituting the known values:
38=27+CQ
Solving for CQ:
CQ=38−27=11cm
Thus, CQ=CR=11cm.
We know that:
CD=CR+RD
Substituting the known values:
25=11+RD
Solving for RD:
RD=25−11=14cm
In quadrilateral OSRD (where O is the center of the circle), we have:
- OS=OR=r (the radius of the circle).
- RD=14cm.
Since ∠D=90∘, triangle OSD is a right triangle with:
- OS as one leg,
- RD as the other leg,
- OD as the hypotenuse.
Since OS=OR and RD is perpendicular to OS, quadrilateral OSRD forms a square. Therefore, all sides are equal:
OS=RD=14cm
Thus, the radius r of the circle is:
r=14cm
The radius r of the circle is 14cm.
Topper's Solved these Questions
- QUADRILATERALBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE
48 Videos
- PROFIT & LOSSBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions
200 Videos
- RATIO & PROPORTIONBOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS
113 Videos
Similar Questions
ABCD is a quadrilateral such that ∠D=90∘. A circle with centre O touches the sides AB, BC and CD and DA at P, Q, R and S respectively. If BC = 40 cm, BP = 28 cm and CD = 25 cm, then what is the radius of the circle is:
ABCD एक चतुर्भुज है जैसे ∠D=90∘ । केन्द्र O वाला एक वृत्त क्रमशः AB, BC और CD और DA को P, Q,R और S से छूता है। यदि BC = 40 सेमी, BP = 28 सेमी और CD = 25 सेमी है, तो वृत्त का त्रिज्या क्या है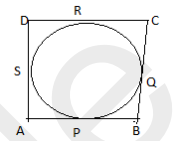
View SolutionIn the given figure, ABCD is a quadrilateral in which ∠D=90∘. A circle C(O,r) touches the side AB, BC, CD and DA at P,Q,R and S, respectively. If BC= 38 cm, CD = 25 cm and BP = 27 cm, then find the value of r.
View Solution
Knowledge Check
A quadrilateral ABCD is drawn to circumscribe a circle such that its sides. AB , BC ,CD and DA touch the circle at P,Q,R and S , respectively . If AB = x cm BC = 7 cm , CR = 3 cm and AS = 5 cm , then x= ?
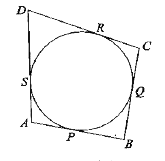 A10 cmB8 cmC9 cmD7 cm
A10 cmB8 cmC9 cmD7 cm
In the given figure, ABCD is a quadrilateral in which ∠D=90. A circle C(O,r) touches the sides AB,BC,CD,DA at P,Q,R and S respectively. If BC=38 cm, CD=25 cm, and BP=27 cm, then find the value of r.
View SolutionABCD is a quadrilateral such that ∠D=90∘. A circle C of radius r touches the sides AB, BC, CD and DA at P, Q, R and S respectively. If BC = 38 cm, CD = 25 cm and BP = 27 cm. Find r
View SolutionIn figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3cm and AS = 5cm, then x = ______.

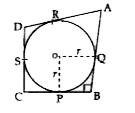
View SolutionIn the following figure ,a circle with centre O is inscribed in a quadrilateral ABCD such that ,it touches the sides BC, AB, AD and CD at points P,Q , R and S respectively .If AB =29 cm , AD =23 cm ∠B=90∘andDS=5 cm.
Find the value of DR :
View SolutionA circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR = 7 cm and CR = 5 cm, then find the length of BC.
View SolutionA circle is inscribed in a quadrilateral ABCD , touching sides AB , BC , CD and DA at P , Q , R , and S respectively. If AS = 8 cm , BC = 11 cm and CR = 5 cm, then the length AB is equal to :
एक वृत्त किसी चतुर्भुज ABCD के भीतर स्थित है जो भुजा AB, BC, CD तथा DA को क्रमशः P, Q, R और S पर स्पर्श करता है | यदि AS = 8 सेमी, BC = 11 सेमी और CR =5 सेमी है, तो AB की लंबाई ज्ञात करें |
View SolutionIn Fig. 2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB=29 cm, AD-23 cm,∠B=90° and DS = 5 cm, then the radius of the circle (in cm)
View Solution
