Question

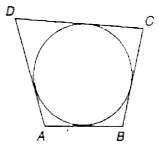
A circle touches the sides of a quadrilateral ABCD at P, Q, R and S respectively. Find the angles subtended at the centre by a pair of opposite sides.

Options

A. `180^(@)`
B. `270^(@)`
C. `225^(@)`
D. None of these

Answer

A

Explanation

To find the angles subtended at the center by a pair of opposite sides of a quadrilateral ABCD, where a circle touches the sides at points P, Q, R, and S, we can follow these steps:

1. Understanding the Configuration:
We have a quadrilateral ABCD with a circle inscribed in it. The points where the circle touches the sides are P (on AB), Q (on BC), R (on CD), and S (on DA).

2. Labeling the Angles:
Let O be the center of the circle. We will denote the angles subtended at the center O by the sides of the quadrilateral as follows:
- Angle AOB for side AB
- Angle BOC for side BC
- Angle COD for side CD
- Angle DOA for side DA

3. Using the Properties of Tangents:
From the properties of tangents, we know that the angles subtended by the tangents from a point outside the circle to the points of tangency are equal. Therefore:
- Angle AOP = Angle AOB
- Angle BQO = Angle BOC
- Angle CRQ = Angle COD
- Angle DSO = Angle DOA

4. Summing the Angles:
The sum of all angles around point O is 360 degrees. Thus, we can write the equation:
\( \text{Angle AOB} + \text{Angle BOC} + \text{Angle COD} + \text{Angle DOA} = 360^\circ \)

5. Identifying Opposite Angles:
We can pair the opposite angles:
- AOB and COD
- BOC and DOA

6. Setting Up the Equations:
Let:
- Angle AOB = x
- Angle BOC = y
- Angle COD = z
- Angle DOA = w

From the sum of angles, we have:
\( x + y + z + w = 360^\circ \)

Since opposite angles are equal, we can express:
\( x + z = 180^\circ \quad \text{(1)} \)
\( y + w = 180^\circ \quad \text{(2)} \)

7. Conclusion:
From equations (1) and (2), we can conclude that:
- The angles subtended at the center by opposite sides of the quadrilateral are supplementary, meaning:
\( \text{Angle AOB} + \text{Angle COD} = 180^\circ \)
\( \text{Angle BOC} + \text{Angle DOA} = 180^\circ \)

Final Answer:
Thus, the angles subtended at the center by a pair of opposite sides of the quadrilateral ABCD are 180 degrees.