The e.m.f. of one accumulator is e, its internal resistance is r. Find the e.m.f. $ε$ and the internal resistance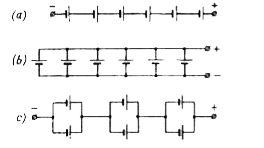
$R_{i}$ of a battery of n accumulators connected (Fig. 26.10):
(a) in series,
(b) in parallel,
(c) in m series-connected groups of k accumulators, $m < n$ .
k = n/m, where the accumulators are connected in parallel.

Text Solution

Verified by Experts

The correct Answer is:(a) $ε = \neq, R_{i} = n r;$ (b) $ε = e; R_{i} = r / n; (c) ε = m e, R_{i} = m r / k, = m^{2} r / n$ .

N cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
AMaximum power is delivered to the load is $K = \sqrt{\frac{N R}{r}}$
BMaximum power is delivered to the load if $K = \sqrt{\frac{r}{N R}}$
CMaximum power delivered to the load is $\frac{E^{2}}{4 N r}$
DMaximum power deliverd to the load is $\frac{N {(E)}^{2}}{4 r}$
A cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
A1/n
B1/(n+1)
Cn/(n+1)
D(n+1)/n
A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A $1 / n$
B $\frac{1}{n + 1}$
C $\frac{n}{n = 1}$
D $\frac{n + 1}{n}$