Describe an experiment to determine the coefficient of thermal conductivity of a good conductor by Searle's method.
Step-by-Step Solution to Determine the Coefficient of Thermal Conductivity by Searle's Method
Step 1: Setup the Apparatus
- Use a long cylindrical bar made of the material whose thermal conductivity you want to measure.
- Attach a steam inlet at one end of the bar to heat it and a water inlet at the other end to cool it.
- Ensure that the bar is well insulated to minimize heat loss to the surroundings.
Hint: Make sure the bar is straight and has a uniform cross-section to ensure accurate measurements.
---
Step 2: Measure Initial Temperatures
- Before starting the experiment, measure the initial temperatures of the steam and the water.
- Record the temperature of the bar at both ends (heated and cooled) using thermometers.
Hint: Use precise thermometers to ensure accurate temperature readings.
---
Step 3: Start Heating and Cooling
- Allow steam to flow into one end of the bar while simultaneously allowing cold water to flow into the other end.
- Maintain a steady flow of steam and water to ensure constant temperature conditions.
Hint: Ensure that the flow rates of steam and water are constant throughout the experiment.
---
Step 4: Measure Heat Transfer
- After a certain time interval (Δt), measure the temperature change of the water (ΔT_water) as it passes through the bar.
- Also, measure the mass of the water (Δm) that has passed through during this time interval.
Hint: Use a graduated cylinder to accurately measure the volume of water collected, and convert it to mass using the density of water.
---
Step 5: Calculate Heat Absorbed by Water
- Use the formula for heat absorbed by the water:
ΔQwater=Cw⋅Δm⋅ΔTwater
where Cw is the specific heat capacity of water.
Hint: The specific heat capacity of water is approximately 4.186J/g°C.
---
Step 6: Calculate Heat Conducted through the Bar
- The heat conducted through the bar can be expressed as:
ΔQbar=−k⋅A⋅ΔTbarL⋅Δt
where k is the thermal conductivity, A is the cross-sectional area of the bar, ΔTbar is the temperature difference across the bar, and L is the length of the bar.
Hint: Ensure that you calculate the cross-sectional area correctly based on the dimensions of the bar.
---
Step 7: Equate Heat Transfer Expressions
- Since there is no heat loss, equate the heat absorbed by the water to the heat conducted through the bar:
Cw⋅Δm⋅ΔTwater=k⋅A⋅ΔTbarL⋅Δt
Hint: Rearranging the equation will help isolate k.
---
Step 8: Solve for Thermal Conductivity (k)
- Rearranging the equation gives:
k=Cw⋅Δm⋅ΔTwater⋅LA⋅ΔTbar⋅Δt
Hint: Make sure to substitute all values with correct units to maintain consistency.
---
Step 9: Record and Analyze Results
- Record the calculated value of k and compare it with standard values for the material to check for accuracy.
Hint: Repeat the experiment multiple times to ensure reliability and average the results for better accuracy.
---
- Use a long cylindrical bar made of the material whose thermal conductivity you want to measure.
- Attach a steam inlet at one end of the bar to heat it and a water inlet at the other end to cool it.
- Ensure that the bar is well insulated to minimize heat loss to the surroundings.
- Before starting the experiment, measure the initial temperatures of the steam and the water.
- Record the temperature of the bar at both ends (heated and cooled) using thermometers.
- Allow steam to flow into one end of the bar while simultaneously allowing cold water to flow into the other end.
- Maintain a steady flow of steam and water to ensure constant temperature conditions.
- After a certain time interval (Δt), measure the temperature change of the water (ΔT_water) as it passes through the bar.
- Also, measure the mass of the water (Δm) that has passed through during this time interval.
- Use the formula for heat absorbed by the water:
ΔQwater=Cw⋅Δm⋅ΔTwater
where Cw is the specific heat capacity of water.
- The heat conducted through the bar can be expressed as:
ΔQbar=−k⋅A⋅ΔTbarL⋅Δt
where k is the thermal conductivity, A is the cross-sectional area of the bar, ΔTbar is the temperature difference across the bar, and L is the length of the bar.
- Since there is no heat loss, equate the heat absorbed by the water to the heat conducted through the bar:
Cw⋅Δm⋅ΔTwater=k⋅A⋅ΔTbarL⋅Δt
- Rearranging the equation gives:
k=Cw⋅Δm⋅ΔTwater⋅LA⋅ΔTbar⋅Δt
- Record the calculated value of k and compare it with standard values for the material to check for accuracy.
Topper's Solved these Questions
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SHORT ANSWER QUESTIONS
19 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - VERY SHORT ANSWER QUESTIONS
5 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
8 Videos
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D
6 Videos
- THERMAL RADIATION BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
14 Videos
Similar Questions
SI unit of coefficient of thermal conductivity
View SolutionThe dimensions of coefficient of thermal conductivity is
View SolutionCoefficient of thermal conductivity has the dimensions:
View SolutionExplain Poiseuille's formula for the volume of liquid flowing through a capillary tube - Describe an experiment to determine the coefficient of viscosity of a liquid by Poiseuiles formula.
View SolutionWrite the coefficient of thermal coonductivity of a perfect heat conductor and that of a perfect heat insulator.
View SolutionExplain Lee's disc method of finding the thermal conductivity of a bad conductor.
View SolutionDefine coefficient of thermal conductivity or thermal conductivity of a substance.
View SolutionIn an experiment to determine the thermal conductivity of copper with Searle's apparatus, 100 gm of water flowed in 4.2 minutes past the cold end of the copper bar, its initial and final temperatures being 25°C and 52°C respectively. If the temperature difference between two points in the bar 10 cm apart is 23°C and the area of cross-section of the bar is 5 cm2, calculate the coefficient of thermal conductivity of copper. Specific heat capacity of water 4,200J kg−1K−1
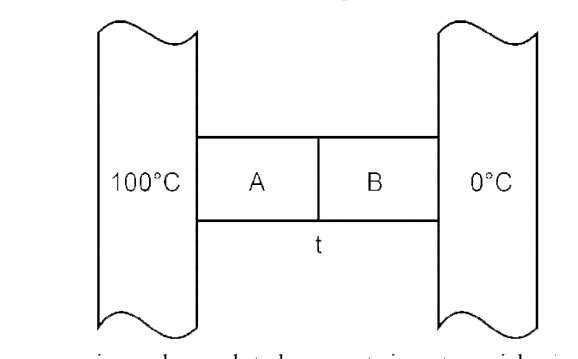
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionIn an experiment to determine the coefficient of viscosity of a liquid using the formual η=πPr48lQ the radius of the capillary tube was measured to be 0.41 mm using an instrument of least count 0.001 cm, length l was measured usinga metre scale as 15 cm. The percentae error in the pressure difference is 0.4% and the percentage error in the volume of the liquid flow out per second Q is 0.3% what is the maximum percentage error in the coefficient of viscosity?
View Solution
