What is the period of oscillation of a liquid contained in a U - tube executing shm ?
To find the period of oscillation of a liquid contained in a U-tube executing simple harmonic motion (SHM), we can follow these steps:
1. Understanding the Setup:
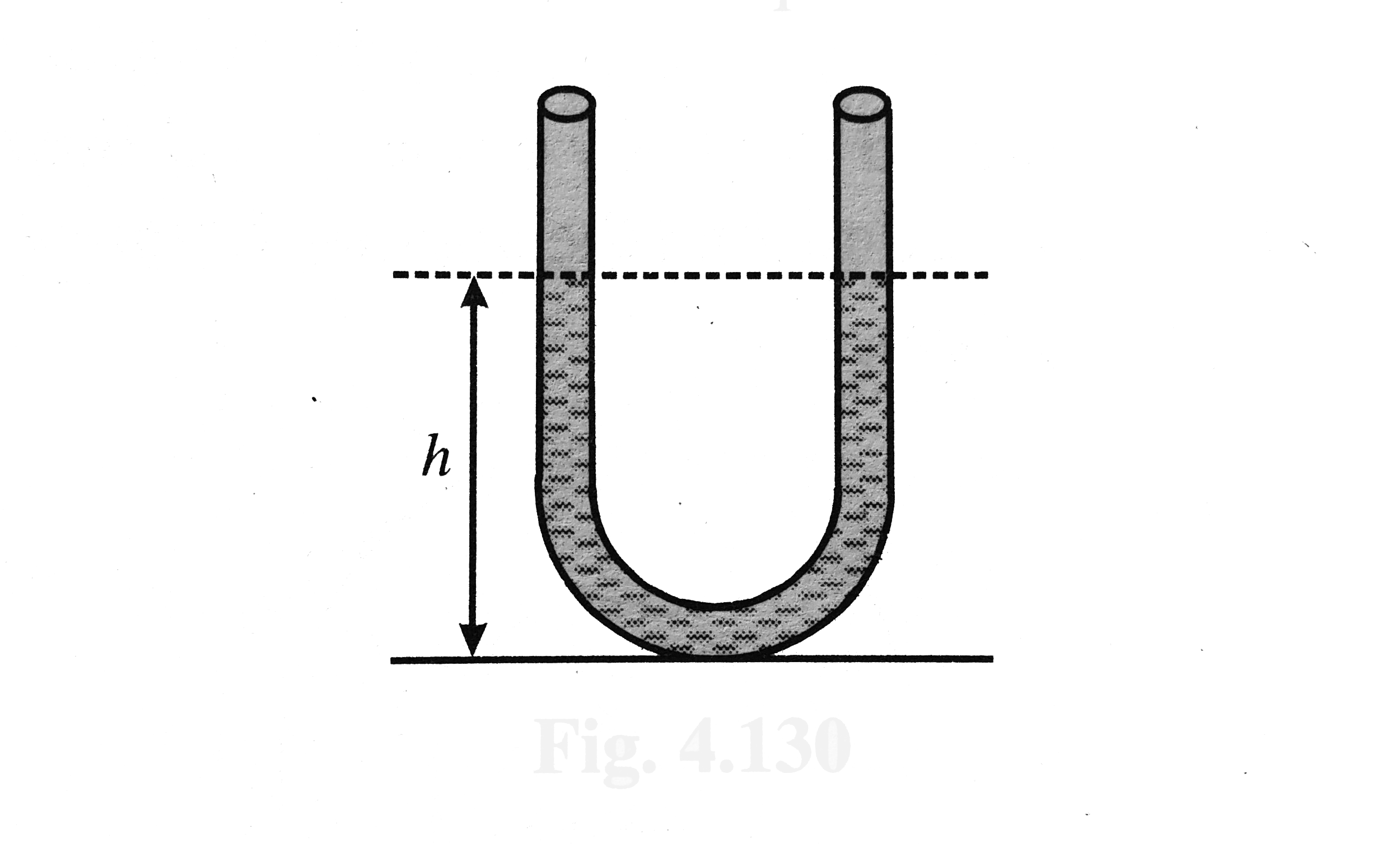
- We have a U-tube filled with liquid. When the liquid is displaced by a distance y, the height of the liquid on one side decreases by y and increases by y on the other side.
2. Defining the Variables:
- Let A be the cross-sectional area of the U-tube.
- Let ρ be the density of the liquid.
- The total length of liquid on both sides of the U-tube is 2L.
3. Calculating the Mass of the Liquid:
- The mass m of the liquid in the U-tube can be expressed as:
m=ρ×Volume=ρ×A×2L
4. Finding the Restoring Force:
- The restoring force FR acting on the liquid due to the displacement y is equal to the weight of the liquid displaced. The volume of the displaced liquid on both sides is 2Ay.
- Therefore, the restoring force can be calculated as:
FR=Weight of displaced liquid=ρ×(2Ay)×g=2ρAgy
- Note that the restoring force acts in the opposite direction to the displacement, hence it is negative:
FR=−2ρAgy
5. Using the SHM Formula:
- In SHM, the restoring force is proportional to the displacement:
F=−ky
- Here, k (the spring constant equivalent for this system) can be identified as 2ρAg.
6. Calculating the Time Period:
- The time period T of SHM is given by:
T=2π√mk
- Substituting m and k:
T=2π√ρ⋅2A⋅L2ρAg=2π√Lg
7. Conclusion:
- The period of oscillation of the liquid in the U-tube is:
T=2π√Lg
- This shows that the period is independent of the density of the liquid.
- We have a U-tube filled with liquid. When the liquid is displaced by a distance y, the height of the liquid on one side decreases by y and increases by y on the other side.
- Let A be the cross-sectional area of the U-tube.
- Let ρ be the density of the liquid.
- The total length of liquid on both sides of the U-tube is 2L.
- The mass m of the liquid in the U-tube can be expressed as:
m=ρ×Volume=ρ×A×2L
- The restoring force FR acting on the liquid due to the displacement y is equal to the weight of the liquid displaced. The volume of the displaced liquid on both sides is 2Ay.
- Therefore, the restoring force can be calculated as:
FR=Weight of displaced liquid=ρ×(2Ay)×g=2ρAgy
- Note that the restoring force acts in the opposite direction to the displacement, hence it is negative:
FR=−2ρAgy
- In SHM, the restoring force is proportional to the displacement:
F=−ky
- Here, k (the spring constant equivalent for this system) can be identified as 2ρAg.
- The time period T of SHM is given by:
T=2π√mk
- Substituting m and k:
T=2π√ρ⋅2A⋅L2ρAg=2π√Lg
- The period of oscillation of the liquid in the U-tube is:
T=2π√Lg
- This shows that the period is independent of the density of the liquid.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - VERY SHORT ANSWER QUESTIONS
13 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM THE CHARACTERISTIC OF SHM)
14 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Motion of an oscillating liquid column in a U-tube is
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View Solution
Knowledge Check
Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonic.Bnon-periodicCsimple harmonic and time period is independent of the density of the liquid.Dsimple harmonic and time period is directly proportional to the density of the liquid.Motion of an oscillating liquid column in a U-tube is
Aperiodic but not simple harmonic.Bnon-periodicCsimple harmonic and time period is independent of the density of the liquid.Dsimple harmonic and time period is directly proportional to the density of the liquid.
The north pole of a very strong electromagnet is brought near the meniscus of a liquid contained in a narrow. U - tube . The liquid is seen to rise towards the north pole. This indicates that the liquid is
View SolutionThe period of oscillation of a liquid in a U. Tube is one to be T1 The first liquid is replaced by another are of higher density. Will there be any change in the period ?
View SolutionObtain an expression for the period of oscillations of a mass attached to end of a spring and undergoing shm. Obtain expression for K.E. and P.E. at any position during shm.
View SolutionWrite down the expression for the period of oscillation of a light piece of cork floating in a liquid .
View SolutionThe bob of simple pendulum executes SHM in water with a period T, while the period of oscillation of the bob is T0 in air. Neglecting frictional force of water and given that the density of the bob is 40003kgm−3 , find the ration between T and T0.
View SolutionConsider a liquid which fills a uniform U - tube uniform U- tube, as shown in figure , up to a height h. Find angular the frequency of small oscillation of th eliquid in the U - tube.
View Solution
