Two pendulums of lengths 1.44 m and 1 m start oscillating together. After how many oscillations will Activate they again start swinging together?
To solve the problem of when the two pendulums will swing together again, we can follow these steps:
Step 1: Understand the formula for the period of a pendulum
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
Step 2: Calculate the time period for both pendulums
For the first pendulum with length L1=1.44m:
T1=2π√1.44g
For the second pendulum with length L2=1m:
T2=2π√1g
Step 3: Find the ratio of the periods
To find out when they will be in phase again, we need to find the least common multiple (LCM) of their periods. First, we can express the periods in terms of their ratio:
T1T2=2π√1.44g2π√1g=√1.44=1.2
Step 4: Set up the equation for synchronization
Let n1 be the number of oscillations of the first pendulum and n2 be the number of oscillations of the second pendulum when they next swing together:
n1T1=n2T2
Substituting the periods:
n1⋅2π√1.44g=n2⋅2π√1g
This simplifies to:
n1√1.44=n2
or
n2=1.2n1
Step 5: Find the smallest integers n1 and n2
To find the smallest integers n1 and n2 that satisfy this equation, we can express n1 in terms of a common integer n:
n1=nandn2=1.2n
To make n2 an integer, n must be a multiple of 5 (since 1.2n must be an integer).
Step 6: Calculate the number of oscillations
The smallest value for n that satisfies this is n=5:
n1=5andn2=1.2×5=6
Thus, after 5 oscillations of the first pendulum, the two pendulums will swing together again.
Final Answer
The two pendulums will swing together again after 5 oscillations of the first pendulum.
---
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
For the first pendulum with length L1=1.44m:
T1=2π√1.44g
T2=2π√1g
To find out when they will be in phase again, we need to find the least common multiple (LCM) of their periods. First, we can express the periods in terms of their ratio:
T1T2=2π√1.44g2π√1g=√1.44=1.2
Let n1 be the number of oscillations of the first pendulum and n2 be the number of oscillations of the second pendulum when they next swing together:
n1T1=n2T2
Substituting the periods:
n1⋅2π√1.44g=n2⋅2π√1g
This simplifies to:
n1√1.44=n2
or
n2=1.2n1
To find the smallest integers n1 and n2 that satisfy this equation, we can express n1 in terms of a common integer n:
n1=nandn2=1.2n
To make n2 an integer, n must be a multiple of 5 (since 1.2n must be an integer).
The smallest value for n that satisfies this is n=5:
n1=5andn2=1.2×5=6
Thus, after 5 oscillations of the first pendulum, the two pendulums will swing together again.
The two pendulums will swing together again after 5 oscillations of the first pendulum.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - VERY SHORT ANSWER QUESTIONS
13 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM THE CHARACTERISTIC OF SHM)
14 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Two pendulums of length 1.21 m and 1.0 m starts vibrationg. At some instant, the two are in the mean position in same phase. After how many vibrations of the longer pendulum, the two will be in phase ?
View SolutionTwo pendulums at rest swinging together. Their lengths are respectively 1.44m and 1m. They will again start swinging in same phase together after (of longer pendulum) :

View Solution
Knowledge Check
Two pendulums differ in lengths by 22m. They oscillate at the same place so that one of then makes 30 oscillations and the other makes 36 oscillations during the same time. The length ( in cm) of the pendulum are :
A1. 72 and 50B2. 60 and 38C3. 50 and 28D4. 80 and 58
Two simple pendulum have lengths land 25l16 . At t=0 they are in same phase after how may oscillations of smaller pendulum will they be again in phase for first time ?
View SolutionTwo simple pendulums of length 0.5 m and 20 m, respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed oscillations.
View SolutionTwo pendulums C and D suspended from a wire as shown in the figure given below. Pendulum C is made to oscillate by displacing it from its mean position. It is seen that D also starts oscillating.
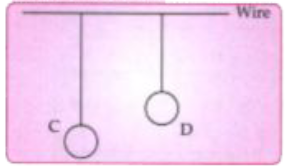
(i) Name the type of oscillation, C will execute.
(ii) Name the type of oscillation, D will execute.
(iii) If the length of D is made equal to C then what difference will you notice in the oscillations of D?
(iv) What is the name of the phenomenon when the length of D is made equal to C?
View SolutionTwo simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
View SolutionTwo pendulums differ in lengths by 22m. They oscillate at the same place so that one of then makes 30 oscillations and the other makes 36 oscillations during the same time. The length ( in cm) of the pendulum are :
View SolutionTwo simple pendulums A and B have lengths 1.0 m and 4.0 m respectively at a certain place. Which pendulum will make more oscillations in 1 minute ? Explain your answer.
View SolutionTwo pendulum of time periods 3 s and 7 s respectively start oscillating simultaneously from two opposite extreme positions. After how much time they will be in same phase?
View Solution