What is γ ? Obtain the value of γ for (i) monatomic (ii) diatomic and (iii) triatomic gas.
Step by step video & image solution for What is γ ? Obtain the value of γ for (i) monatomic (ii) diatomic and (iii) triatomic gas. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - VERY SHORT ANSWER QUESTIONS17videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM FIRST LAW OF THERMODYNAMICS )6videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - LONG ANSWER QUESTIONS8videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
Similar Questions
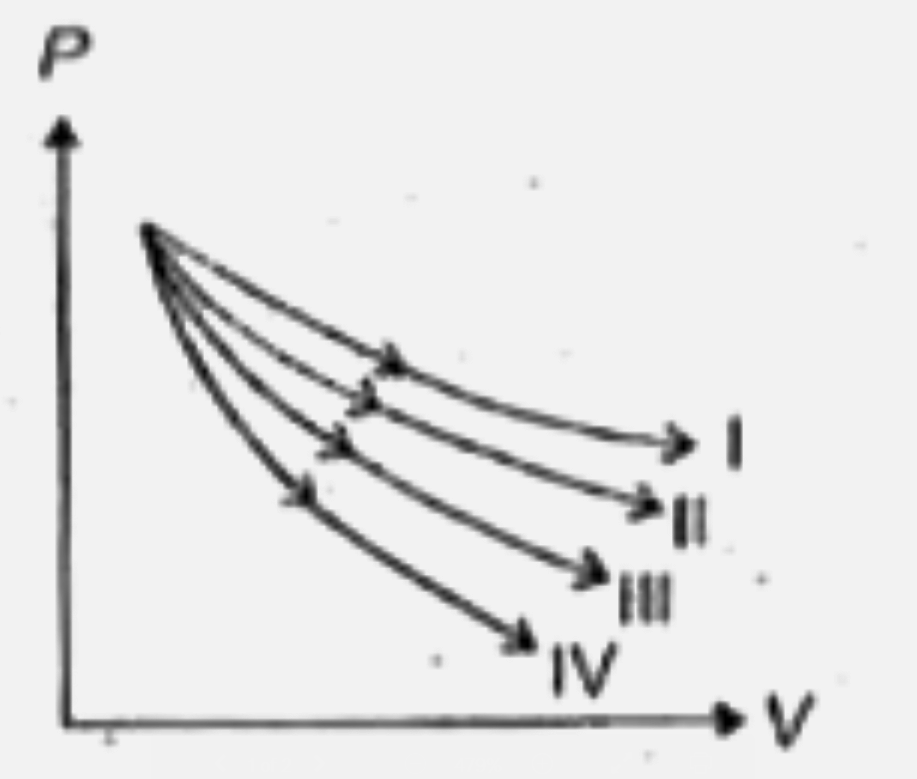
In the following plots match I,II, III,Iv with (a) isothermal process and Adiabatic process for (b) monatomic, (c ) diatomic and (d) triatomic gases respectively.
View SolutionWhat are (i) audible frequency, (ii) infra-sonics and (iii) ultra-sonics ?
View SolutionValue of Cp for monatomic gas is 52R. Find CV.
View SolutionFind the values of the following :
(i) i73
(ii) i−6
(iii) 1iView SolutionThe value of CV for monatomic gas is 32R, then CP will be
View SolutionThe straight lines in the figure depict the variations in temperature ΔT as a function of the amount of heat supplied Q is different process involving the change of state of a monoatomic and a diatomic ideal gas . The initial states, (P,V,T) of the two gases are the same . Match the processes as described, with the straight lines in the graph as numbered.
_E01_155_Q01.png)
Column-IColumn-II(A)Isobaric process of monoatomic gas.(p)1(B)Isobaric process of diatomic gas(q)2(C)Isochoric process of monoatomic gas(r)Minimum at section B(D)Isochoric process of diatomic gas(s)x-axis (i.e.'Q' axis)View SolutionThe value of γ of linear, arragement of triatomic gas molecules is
View SolutionQ cal of heat is required to raise the temperature of 1 mole of a monatomic gas from 20∘C to 30∘C at constant pressure. The amount of heat required to raise the temperature of 1 mole of diatomic gas form 20∘C to 25∘C
View SolutionThe heat capacity of a diatomic gas is higher than that of a monatomic gas.
View SolutionCompressibility factor, Z of a gas is given as Z=pVnRT
(i) What is the value of Z for an ideal gas ?
(ii) For real gas what will be the effect on value of Z above boyle's temperature ?View Solution