gravitational field strength
Step by step video solution for gravitational field strength by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Density of a planet is two times the density of earth. Radius of this planet is half. Match the following (as compared to earth)
Column-IColumn-II(A)Accleration due to gravity on this planet's surface(p)Half(B)Gravitational potential on the surface(q)Same(C)Gravitational potential at centre(r)Two times(D)Gravitational field strength at centre(s)Four times
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
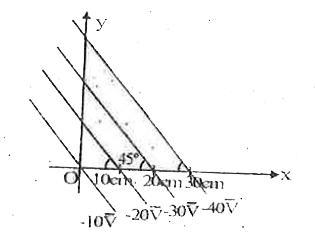
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is
View Solution
Knowledge Check
Assertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
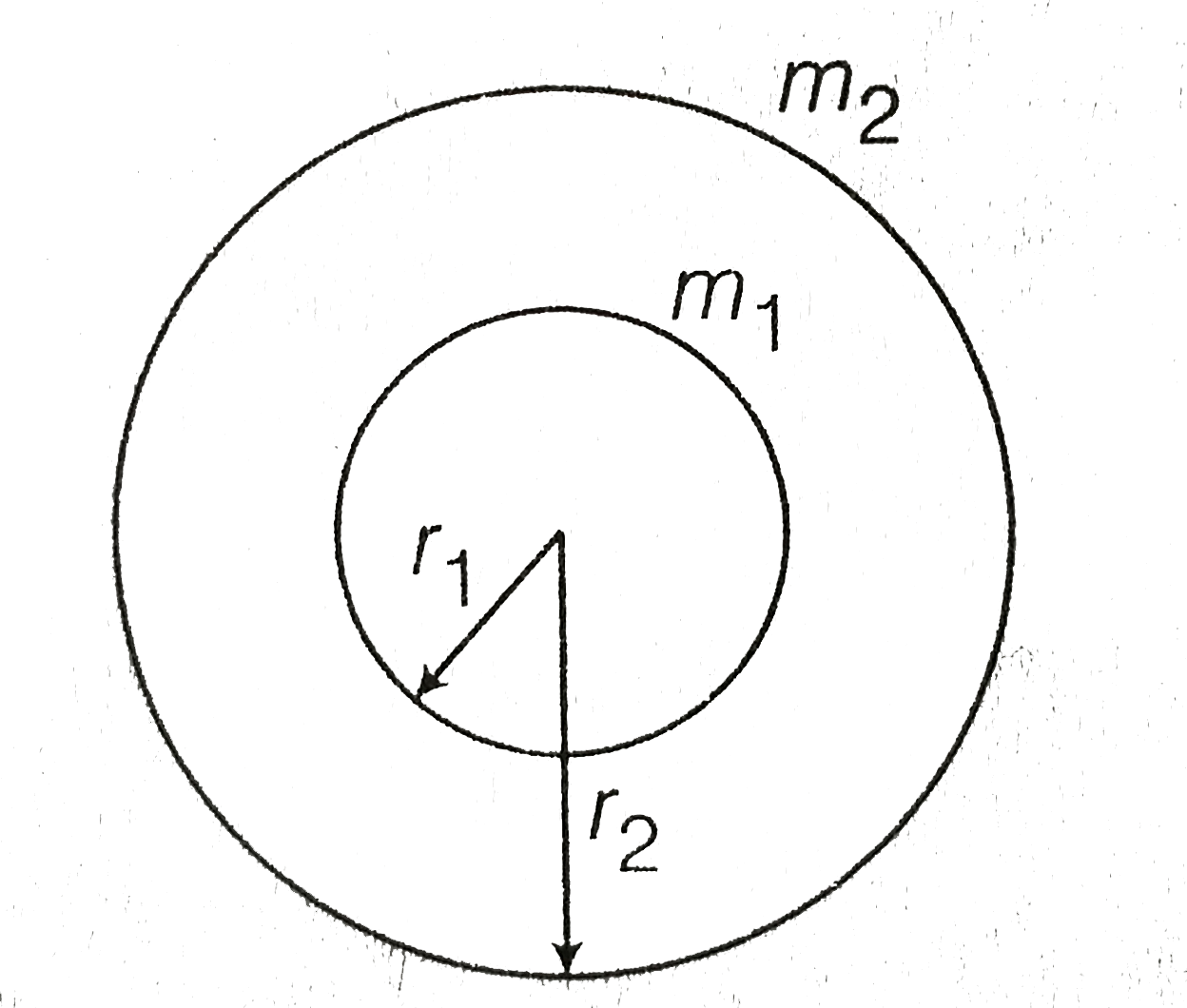
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).AIf both Assertin and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is trueThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
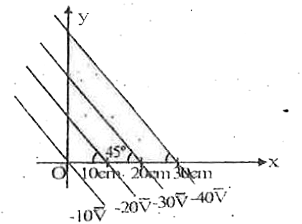
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) isA4cm/sB2cm/sC2√2cmsD1cm/sThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
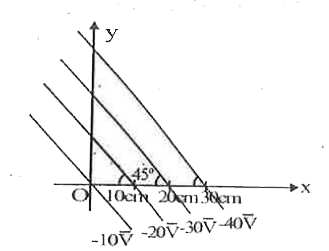
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) isA4cm/sB2cm/sC2√2cmsD1cm/s
The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzhark)

In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v is in cm//s) as function of its y-co ordinate is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
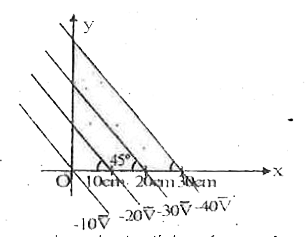
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
y-component of E a the point whose co-ordinates are (4cm,4cm) is
View Solution_E01_017_Q01.png)
A spherical cave of radius R/2 was carved out from a uniform sphere of radius R and original mass M. the center of the cave is at R/2 from the center of the large sphere. Point P is at a distance 2R from the center the large sphere and on the joing line of the two centers. the gravitational field strength g at point P is
View SolutionAssertion : Gravitational potential and gravitational potentail energy, both are related to the work done by gravitational force in the gravitational field
Reason : Gravitational field strength is related to the gravitaional force in gravitational field.
View SolutionThree planets of same density and with radii R1,R2 and R3 such that R1=2R2=3R3 have gravitation fields strength on planets are v1,v2,v3, respectively. Then :
View Solution
