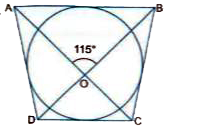
If a quardilateral (ABCD) is circumscribed of a circle and ∠ BOC is 125 then find ∠ AOD
The correct Answer is:8.4xcm
To solve the problem, we need to find the angle ∠AOD in the quadrilateral ABCD that is circumscribed around a circle, given that ∠BOC=125∘.
1. Understanding the Geometry:
- We have a quadrilateral ABCD that is circumscribed around a circle. This means that all its vertices touch the circle.
- The angles BOC and AOD are formed by the diagonals BD and AC intersecting at the center O of the circle.
2. Using the Properties of Angles:
- In a cyclic quadrilateral (a quadrilateral inscribed in a circle), the angles subtended by the same arc are equal.
- The angles ∠BOC and ∠AOD are related because they are both central angles that subtend the arcs BC and AD respectively.
3. Applying the Given Information:
- We know that ∠BOC=125∘.
- According to the properties of cyclic quadrilaterals, the angles ∠AOD and ∠BOC are equal.
4. Conclusion:
- Therefore, we can conclude that ∠AOD=∠BOC=125∘.
Final Answer:
∠AOD=125∘
- We have a quadrilateral ABCD that is circumscribed around a circle. This means that all its vertices touch the circle.
- The angles BOC and AOD are formed by the diagonals BD and AC intersecting at the center O of the circle.
- In a cyclic quadrilateral (a quadrilateral inscribed in a circle), the angles subtended by the same arc are equal.
- The angles ∠BOC and ∠AOD are related because they are both central angles that subtend the arcs BC and AD respectively.
- We know that ∠BOC=125∘.
- According to the properties of cyclic quadrilaterals, the angles ∠AOD and ∠BOC are equal.
- Therefore, we can conclude that ∠AOD=∠BOC=125∘.
∠AOD=125∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
Quadrilateral ABCD is circumscribed to a circle. If AB=6cm, BC=7cm and CD=4cm then the length of AD is
A3cmB4cmC6cmD7cmIf the sides of a quadrilateral ABCD touch a circle and AB = 6 cm, CD = 5 cm, BC = 7 cm, then the length of AD in cm is :
A4 cmB5 cmC3 cmD6 cmIn the given figure, quadrilateral ABCD is circumscribed, touching the circle at P, Q, R and S. If AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm, then perimeter of quadrilateral ABCD is
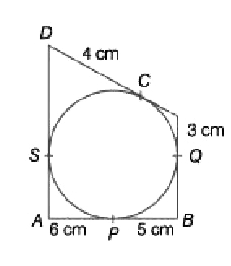 A18 cmB27 cmC36 cmD32 cm
A18 cmB27 cmC36 cmD32 cm
In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD⊥AB. If radius of incircle is 10cm, then the value of x is

View SolutionIn Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD

View SolutionQuadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
View Solution