ABCD is a rectangle where ratio of the length of AB and BC is 3 : 2. If P is the mid point of AB . Find sin ∠CPB
The correct Answer is:45
To find sin∠CPB in rectangle ABCD where the ratio of the lengths of sides AB and BC is 3:2, we can follow these steps:
Step 1: Define the lengths of the rectangle
Let the length of AB be 3x and the length of BC be 2x. Thus, we have:
- AB=3x
- BC=2x
Step 2: Identify the coordinates of the points
Assuming point A is at the origin (0, 0):
- A(0,0)
- B(3x,0)
- C(3x,2x)
- D(0,2x)
Step 3: Find the midpoint P of AB
The midpoint P of segment AB can be calculated as:
P=(0+3x2,0+02)=(3x2,0)
Step 4: Calculate the lengths of sides BC and PC
- The length BC is simply 2x.
- To find the length PC, we use the distance formula:
PC=√(3x−3x2)2+(2x−0)2
Calculating this:
PC=√(3x2)2+(2x)2=√9x24+4x2=√9x24+16x24=√25x24=5x2
Step 5: Apply the sine definition in triangle BCP
In triangle BCP, we know:
sin∠CPB=oppositehypotenuse=BCPC
Substituting the values we found:
sin∠CPB=2x5x2=2x⋅25x=45
Conclusion
Thus, the value of sin∠CPB is:
sin∠CPB=45
---
Let the length of AB be 3x and the length of BC be 2x. Thus, we have:
- AB=3x
- BC=2x
Assuming point A is at the origin (0, 0):
- A(0,0)
- B(3x,0)
- C(3x,2x)
- D(0,2x)
The midpoint P of segment AB can be calculated as:
P=(0+3x2,0+02)=(3x2,0)
- The length BC is simply 2x.
- To find the length PC, we use the distance formula:
PC=√(3x−3x2)2+(2x−0)2
Calculating this:
PC=√(3x2)2+(2x)2=√9x24+4x2=√9x24+16x24=√25x24=5x2
In triangle BCP, we know:
sin∠CPB=oppositehypotenuse=BCPC
Substituting the values we found:
sin∠CPB=2x5x2=2x⋅25x=45
Thus, the value of sin∠CPB is:
sin∠CPB=45
Topper's Solved these Questions
Similar Questions
ABCD is a given rectangle with length as 80 cm and breadth as 60 cm. P. G. R, S are the mid points of sides AB, BC, CD, DA respectively. A circular rangoli of radius 10 cm is drawn at the centre as shown in Fig. 9.69. Find the area of shaded portion.
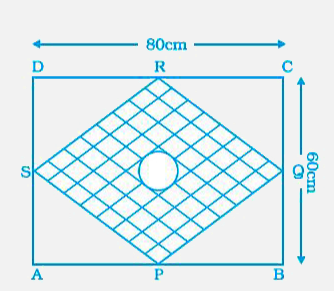
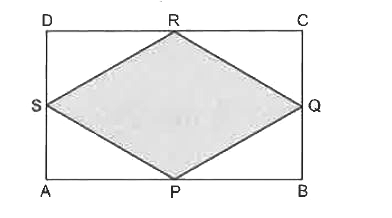
View SolutionIn the given figure, ABCD is a rectangle in which AB = 40 cm and BC = 25 cm. If P. Q, R, S be the midpoints of AB, BC, CD and DA respectively, find the area of the shaded region.
View Solution
Knowledge Check
ABCD is a rectangle where ratio of the length of AB and BC is 3 : 2. If P is the mid point of AB . Find sin ∠CPB
A35B25C34D45In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by ACA ¯¯¯¯¯¯AB is 10.2 cm long. If P is the mid point of AB, then the length of ¯¯¯¯¯¯PB is ____
A4.8 cmB8.2 cmC5.1 cmD5.2 cm
Area of square ABCD is 4 unit2.MandN are mid points of ABandBC. Find PC.
View Solution19. ABCD is a rectangle having length (x 1) and breadth (x- 1). If P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively, then the perimeter of quadrilateral PQRS is
View SolutionIn the given figure, ABCD is a rectangle in AB−40cmandBC=25cm. If P,Q,R,S be the mid-points of the sides AB,BC,CDandDA respectively, find the area of the shaded region.
View SolutionIf C is the mid-point of AB and P is any point outside AB, then
View SolutionIf C is the mid-point of AB and P is any point outside AB, then
View Solution
