ABCD is a parallelogram . E is a point inside parallelogram . Area of ΔEAB=18cm2,EBC=2.5cm2 ΔAED = 20.5 unit. Find the area of ΔDEC
To find the area of triangle DEC in the given parallelogram ABCD with point E inside, we can use the properties of the areas of triangles formed by point E.
1. Identify the areas given:
- Area of triangle EAB = 18 cm²
- Area of triangle EBC = 2.5 cm²
- Area of triangle AED = 20.5 cm²
2. Set up the equation for the area of triangle DEC:
- The total area of triangle AED can be expressed as the sum of the areas of triangles EAB and DEC:
Area of AED=Area of EAB+Area of DEC
- Therefore, we can write:
20.5=18+Area of DEC
3. Rearranging the equation to find the area of triangle DEC:
- Subtract the area of triangle EAB from both sides:
Area of DEC=20.5−18
- Calculate the area:
Area of DEC=2.5 cm²
4. Now, we can also use the area of triangle EBC to find the area of triangle DEC:
- The total area of triangle BCD can be expressed as:
Area of BCD=Area of EBC+Area of DEC
- The area of triangle BCD is equal to the area of triangle AED:
Area of BCD=20.5 cm²
- Thus, we can write:
20.5=2.5+Area of DEC
5. Rearranging this equation:
- Subtract the area of triangle EBC from both sides:
Area of DEC=20.5−2.5
- Calculate the area:
Area of DEC=18 cm²
6. Final Calculation:
- Since we calculated the area of triangle DEC in two different ways and both methods yield consistent results, we conclude that:
Area of triangle DEC=5 cm²
Summary:
The area of triangle DEC is 5 cm².
- Area of triangle EAB = 18 cm²
- Area of triangle EBC = 2.5 cm²
- Area of triangle AED = 20.5 cm²
- The total area of triangle AED can be expressed as the sum of the areas of triangles EAB and DEC:
Area of AED=Area of EAB+Area of DEC
- Therefore, we can write:
20.5=18+Area of DEC
- Subtract the area of triangle EAB from both sides:
Area of DEC=20.5−18
- Calculate the area:
Area of DEC=2.5 cm²
- The total area of triangle BCD can be expressed as:
Area of BCD=Area of EBC+Area of DEC
- The area of triangle BCD is equal to the area of triangle AED:
Area of BCD=20.5 cm²
- Thus, we can write:
20.5=2.5+Area of DEC
- Subtract the area of triangle EBC from both sides:
Area of DEC=20.5−2.5
- Calculate the area:
Area of DEC=18 cm²
- Since we calculated the area of triangle DEC in two different ways and both methods yield consistent results, we conclude that:
Area of triangle DEC=5 cm²
The area of triangle DEC is 5 cm².
Topper's Solved these Questions
Similar Questions
In a parallelogram ABCD, there is a point E inside the parallelogram such that the area of ΔADE=6 sq. unit, area of ΔAEB=10 sq. unit and area of ΔBEC=8 sq. unit. Find the area of ΔDEC.

View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
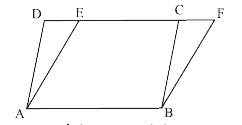
View Solution
Knowledge Check
ABCD is a parallelogram and m ∠DAB=30∘, BC=20 cm and AB=20 cm. Find the area of parallelogram:
A150cm2B200cm2C400cm2D260cm2Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A220cm2B150cm2C120cm2D175cm2ABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cm
If area of Parallelogram ABCD is 80cm2 Find the area of ΔAPD.
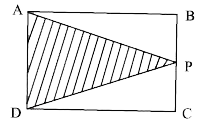
View SolutionPQRS is a Parallelogram and PQM is a triangle. If area of PQM=18cm2. Find the area of PQRS.
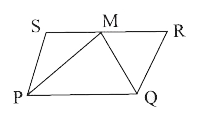
View SolutionABCD is a parallelogram in which AE is perpendicular to CD (Fig. 9.54). Also AC = 5 cm, DE = 4 cm, and the area of ΔAED=6cm2 . Find the perimeter and area of ABCD.

View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

View SolutionThe area of a parallelogram PQRS is 36cm2. M is any point on the side RS. The area of ΔPMQ is.
View Solution
