ABCD is trapezium in which BC∣∣AD BC = 16 AD = 12 . Distance bw/lines =10 cm find area
The correct Answer is:140cm2
To find the area of trapezium ABCD where BC is parallel to AD, we can use the formula for the area of a trapezium:
Area=12×(b1+b2)×h
where b1 and b2 are the lengths of the two parallel sides, and h is the height (the distance between the parallel sides).
1. Identify the lengths of the parallel sides:
- BC=16 cm (this is b1)
- AD=12 cm (this is b2)
2. Identify the height (distance between the parallel sides):
- The distance between the parallel lines is given as h=10 cm.
3. Substitute the values into the area formula:
Area=12×(b1+b2)×h
Area=12×(16+12)×10
4. Calculate b1+b2:
16+12=28
5. Substitute back into the area formula:
Area=12×28×10
6. Calculate 12×28:
12×28=14
7. Now multiply by the height:
14×10=140
8. Final result:
Area=140 cm2
Conclusion:
The area of trapezium ABCD is 140 cm2.
- BC=16 cm (this is b1)
- AD=12 cm (this is b2)
- The distance between the parallel lines is given as h=10 cm.
Area=12×(b1+b2)×h
Area=12×(16+12)×10
16+12=28
Area=12×28×10
12×28=14
14×10=140
Area=140 cm2
The area of trapezium ABCD is 140 cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
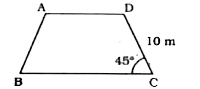 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2m
In the given figure, ABCD is a trapezium in which AB = 9 cm, AD = BC= 6 cm, DC = x cm, and distance between AB and DC is 2√5 cm. The value of area of trapezium ABCD is k√5. Find the value of k.

View SolutionABCD is a trapezium in which AD II BC . AB = 9 cm, BC =12 cm, CD = 15 cm, DA = 20 cm. Find the sum of square of diagonals.
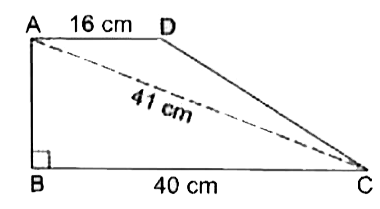
View SolutionIn the given figure, ABCD is a trapezium in which AD∣∣BC,∠ABC=90∘,AD=16cm,AC=41cm and BC = 40 cm. Find the area of the trapezium.
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View SolutionABCDis a trapezium, such that AB=CD and AD∣∣BC.AD=10cmandBC=18cm. If the area of ABCDis 70cm2, what is the value (in cm) of CD?
View Solution
