ABCD is a regular trapezium in which AD∣∣BC Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
To solve the problem, we will use the properties of similar triangles and the given segments of the diagonals in the trapezium ABCD.
1. Identify the Given Information:
- In trapezium ABCD, we have:
- AO=3
- CO=X−3
- BO=3X−19
- DO=X−5
2. Use the Property of Similar Triangles:
- Since AD∥BC, triangles △DAO and △CBO are similar by the Alternate Interior Angles Theorem.
- Therefore, the corresponding sides of these triangles are in proportion:
DOBO=AOCO
3. Substitute the Given Values:
- Substitute the values of AO, CO, DO, and BO into the proportion:
X−53X−19=3X−3
4. Cross-Multiply:
- Cross-multiplying gives us:
(X−5)(X−3)=3(3X−19)
5. Expand Both Sides:
- Expanding the left side:
X2−3X−5X+15=X2−8X+15
- Expanding the right side:
9X−57
6. Set Up the Equation:
- Now we have:
X2−8X+15=9X−57
7. Rearrange the Equation:
- Move all terms to one side:
X2−8X−9X+15+57=0
X2−17X+72=0
8. Factor the Quadratic Equation:
- Factor the quadratic:
(X−9)(X−8)=0
9. Find the Values of X:
- Setting each factor to zero gives:
X−9=0⇒X=9
X−8=0⇒X=8
Conclusion:
The possible values of X are 8 and 9.
- In trapezium ABCD, we have:
- AO=3
- CO=X−3
- BO=3X−19
- DO=X−5
- Since AD∥BC, triangles △DAO and △CBO are similar by the Alternate Interior Angles Theorem.
- Therefore, the corresponding sides of these triangles are in proportion:
DOBO=AOCO
- Substitute the values of AO, CO, DO, and BO into the proportion:
X−53X−19=3X−3
- Cross-multiplying gives us:
(X−5)(X−3)=3(3X−19)
- Expanding the left side:
X2−3X−5X+15=X2−8X+15
- Expanding the right side:
9X−57
- Now we have:
X2−8X+15=9X−57
- Move all terms to one side:
X2−8X−9X+15+57=0
X2−17X+72=0
- Factor the quadratic:
(X−9)(X−8)=0
- Setting each factor to zero gives:
X−9=0⇒X=9
X−8=0⇒X=8
The possible values of X are 8 and 9.
Topper's Solved these Questions
Similar Questions
In the adjoining figure, ABCD is a trapezium in which CD∣∣AB and its diagonals intersect at O. if AO=(5x−7)cm,OC=(2x+1)cm,BO=(7x−5)cmandOD=(7x+1)cm, find the value of x.
View SolutionIn the given figure, ABCD is trapezium whow diagonals AC and BD intersect at O such that OA=(3x−1)cm,(OB=(2x+1)cm,OC=(5x−3)cmandOD=(6x−5)cm. Then, x=?

View Solution
Knowledge Check
ABCD is a regular trapezium in which AD∣∣BC Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
A−8,9B8,−9C−8,−9D8,9ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A1:4B2:3C1:2D1:3
ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionABCD is an isoceles trapezium . AB||CD AD=BC diagonal intersect at O, area of ABO = 84cm2 find area of ΔCOD
View SolutionIn trapezium ABCD side AB∣∣ side DC, diagonals AC and BD intersect In point O. If AB=20,DC=6,OB=15 thn find OD.
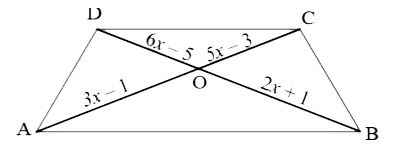
View SolutionIn the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other as the point O. Show that AOBO=CODO.
View Solution
