Question

The distance between the two atoms in a diatomic molecule $O_2$ is $1.21\times {10}^{-10}$ m. The mass of each oxygen atom is $2.66\times {10}^{-26}$ kg. Treating the atoms as point masses find the m moment of inertia of the molecule about an axis passing perpendicular to the line joining the centres of the atoms.

Explanation

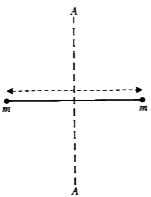
Let the distance between the two atoms be r.
Mass of each atom, `m=2.66 xx 10^(-26)` kg

`r = 1.21 xx 10^(-10) m`
M.I. of the two atoms about the axis AB
`=m(r/2)^(2) + m(r/2)^(2) = 2 xx (mr^(2))/4 =1/2 mr^(2)`
`=(2.66 xx 10^(-26) xx (1.21 xx 10^(-10))^(2))/2`
`=1.95 xx 10^(-46) kg m^(2)`