How is the distance related with time for the motion under uniform acceleration such as the motion of a freely falling body?
To find the relationship between distance and time for the motion of a freely falling body under uniform acceleration, we can use the equations of motion. Here's a step-by-step solution:
Step 1: Understand the scenario
A freely falling body is subject to uniform acceleration due to gravity. The acceleration a is equal to g, the acceleration due to gravity, which is approximately 9.81m/s2 (we will use g as a constant).
Step 2: Identify initial conditions
For a freely falling body, we assume:
- Initial velocity u=0 (the body starts from rest).
- Acceleration a=g (the body accelerates downwards).
Step 3: Use the equation of motion
We will use the second equation of motion:
s=ut+12at2
Substituting the values of u and a:
s=0⋅t+12gt2
This simplifies to:
s=12gt2
Step 4: Analyze the relationship
From the equation s=12gt2, we can see that:
- The distance s is directly proportional to the square of the time t2.
- This means that as time increases, the distance increases with the square of that time.
Conclusion
The relationship between distance and time for a freely falling body under uniform acceleration is given by:
s∝t2
This indicates that the distance traveled by the body is proportional to the square of the time taken.
---
A freely falling body is subject to uniform acceleration due to gravity. The acceleration a is equal to g, the acceleration due to gravity, which is approximately 9.81m/s2 (we will use g as a constant).
For a freely falling body, we assume:
- Initial velocity u=0 (the body starts from rest).
- Acceleration a=g (the body accelerates downwards).
We will use the second equation of motion:
s=ut+12at2
Substituting the values of u and a:
s=0⋅t+12gt2
This simplifies to:
s=12gt2
From the equation s=12gt2, we can see that:
- The distance s is directly proportional to the square of the time t2.
- This means that as time increases, the distance increases with the square of that time.
The relationship between distance and time for a freely falling body under uniform acceleration is given by:
s∝t2
This indicates that the distance traveled by the body is proportional to the square of the time taken.
Topper's Solved these Questions
- MOTION IN ONE DIMENSION BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (B) ( Multiple choice type :)
3 Videos
- MOTION IN ONE DIMENSION BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (B) ( Numericals )
12 Videos
- MOTION IN ONE DIMENSION BOOK - ICSECHAPTER - MOTION IN ONE DIMENSION EXERCISE - EXERCISE -2 (A) ( Numericals )
16 Videos
- MEASUREMENTS AND EXPERIMENTATION BOOK - ICSECHAPTER - MEASUREMENTS AND EXPERIMENTATION EXERCISE - TOPIC 2 SIMPLE PENDULUM (4 Marks Questions )
1 Videos
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBOOK - ICSECHAPTER - PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREEXERCISE - Exercise -4(B)Numericals
5 Videos
Similar Questions
Knowledge Check
Position-time graph for motion with zero acceleration is
A B
B C
C D
D
How is molecular motion related with temperature?
View SolutionPosition - time graph for motion with negative acceleration is
View SolutionDifferentiate between uniform linear motion and uniform circular motion.
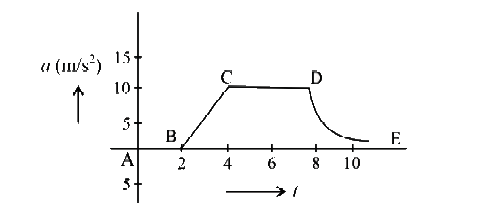
View SolutionThe uniform motion in the following acceleration-time graph is
View SolutionHow does uniform circular motion differ from uniform linear motion ?
View SolutionDraw velocity – time graph of uniformly accelerated motion in one dimension. From the velocity – time graph of uniform accelerated motion, deduce the equations of motion in distance and time.
View SolutionIn a uniform circular motion, the centripetal acceleration is
View Solution
