An insect is crawling up on a vertical wall. It crawls up 1257 inch. Then it slips back 31114 inch and then again crawls up 516 inch. How far is it from the starting point?
11625 inch
12221 inch
14221 inch
13528 inch
The correct Answer is:C
To solve the problem step by step, we will follow these steps:
Step 1: Convert Mixed Numbers to Improper Fractions
1. Crawling Up: The insect crawls up 1257 inches.
- Convert to improper fraction:
\(
12 \frac{5}{7} = \frac{12 \times 7 + 5}{7} = \frac{84 + 5}{7} = \frac{89}{7}
\)
2. Slipping Back: The insect slips back 31114 inches.
- Convert to improper fraction:
\(
3 \frac{11}{14} = \frac{3 \times 14 + 11}{14} = \frac{42 + 11}{14} = \frac{53}{14}
\)
3. Crawling Up Again: The insect crawls up 516 inches.
- Convert to improper fraction:
\(
5 \frac{1}{6} = \frac{5 \times 6 + 1}{6} = \frac{30 + 1}{6} = \frac{31}{6}
\)
Step 2: Calculate the Total Distance from the Starting Point
Now we will calculate the total distance the insect has crawled up and slipped back:
\(
\text{Total Distance} = \left(\frac{89}{7} - \frac{53}{14} + \frac{31}{6}\right)
\)
Step 3: Find the Least Common Multiple (LCM)
To add and subtract these fractions, we need to find the LCM of the denominators (7, 14, and 6):
- Prime factors:
- 7: \(7\)
- 14: \(2 \times 7\)
- 6: \(2 \times 3\)
- LCM: \(2 \times 3 \times 7 = 42\)
Step 4: Convert Each Fraction to Have a Common Denominator
1. Convert \(\frac{89}{7}\) to have a denominator of 42:
\(
\frac{89}{7} = \frac{89 \times 6}{42} = \frac{534}{42}
\)
2. Convert \(\frac{53}{14}\) to have a denominator of 42:
\(
\frac{53}{14} = \frac{53 \times 3}{42} = \frac{159}{42}
\)
3. Convert \(\frac{31}{6}\) to have a denominator of 42:
\(
\frac{31}{6} = \frac{31 \times 7}{42} = \frac{217}{42}
\)
Step 5: Combine the Fractions
Now we can combine the fractions:
\(
\frac{534}{42} - \frac{159}{42} + \frac{217}{42} = \frac{534 - 159 + 217}{42}
\)
Calculating the numerator:
\(
534 - 159 + 217 = 534 + 217 - 159 = 592
\)
Thus, we have:
\(
\frac{592}{42}
\)
Step 6: Simplify the Fraction
Now we simplify \(\frac{592}{42}\):
- Divide both the numerator and the denominator by 2:
\(
\frac{592 \div 2}{42 \div 2} = \frac{296}{21}
\)
Step 7: Convert to Mixed Number
Convert \(\frac{296}{21}\) to a mixed number:
- Divide 296 by 21:
\(
296 \div 21 = 14 \quad \text{(whole number)}
\)
- Remainder:
\(
296 - (21 \times 14) = 296 - 294 = 2
\)
Thus, we have:
\(
14 \frac{2}{21}
\)
Final Answer
The insect is \(14 \frac{2}{21}\) inches from the starting point.
---
1. Crawling Up: The insect crawls up 1257 inches.
- Convert to improper fraction:
\(
12 \frac{5}{7} = \frac{12 \times 7 + 5}{7} = \frac{84 + 5}{7} = \frac{89}{7}
\)
- Convert to improper fraction:
\(
3 \frac{11}{14} = \frac{3 \times 14 + 11}{14} = \frac{42 + 11}{14} = \frac{53}{14}
\)
- Convert to improper fraction:
\(
5 \frac{1}{6} = \frac{5 \times 6 + 1}{6} = \frac{30 + 1}{6} = \frac{31}{6}
\)
Now we will calculate the total distance the insect has crawled up and slipped back:
\(
\text{Total Distance} = \left(\frac{89}{7} - \frac{53}{14} + \frac{31}{6}\right)
\)
To add and subtract these fractions, we need to find the LCM of the denominators (7, 14, and 6):
- Prime factors:
- 7: \(7\)
- 14: \(2 \times 7\)
- 6: \(2 \times 3\)
- LCM: \(2 \times 3 \times 7 = 42\)
1. Convert \(\frac{89}{7}\) to have a denominator of 42:
\(
\frac{89}{7} = \frac{89 \times 6}{42} = \frac{534}{42}
\)
\(
\frac{53}{14} = \frac{53 \times 3}{42} = \frac{159}{42}
\)
\(
\frac{31}{6} = \frac{31 \times 7}{42} = \frac{217}{42}
\)
Now we can combine the fractions:
\(
\frac{534}{42} - \frac{159}{42} + \frac{217}{42} = \frac{534 - 159 + 217}{42}
\)
Calculating the numerator:
\(
534 - 159 + 217 = 534 + 217 - 159 = 592
\)
Thus, we have:
\(
\frac{592}{42}
\)
Now we simplify \(\frac{592}{42}\):
- Divide both the numerator and the denominator by 2:
\(
\frac{592 \div 2}{42 \div 2} = \frac{296}{21}
\)
Convert \(\frac{296}{21}\) to a mixed number:
- Divide 296 by 21:
\(
296 \div 21 = 14 \quad \text{(whole number)}
\)
- Remainder:
\(
296 - (21 \times 14) = 296 - 294 = 2
\)
Thus, we have:
\(
14 \frac{2}{21}
\)
The insect is \(14 \frac{2}{21}\) inches from the starting point.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FRACTIONSEXERCISE - Warm-up Exercise24videos
FRACTIONS
- BOOK - ICSECHAPTER - FRACTIONSEXERCISE - Exercise 2.114videos
FRACTIONS
- BOOK - ICSECHAPTER - FRACTIONSEXERCISE - Example52videos
FRACTIONS
- BOOK - ICSECHAPTER - EXPONENTS AND POWERSEXERCISE - Unit practice paper -17videos
EXPONENTS AND POWERS
- BOOK - ICSECHAPTER - FUNDAMENTAL GEOMETRICAL CONCEPTSEXERCISE - Exercise14videos
FUNDAMENTAL GEOMETRICAL CONCEPTS
Similar Questions
An insect is at a point A on a wall. It crawls up 3 inches and thenn slides down by 6 inches. The insect then again crawls up 5 inches. How many inches above or below the point A is the insect now?
View SolutionA centipede was crawling in a straight line. First it crawled for 837 inch, then it crawled in the reverse direction for 558 inch. Once again it reversed direction and crawled for 1112 inch in the original direction. How far away was it finally from the starting point?
View Solution
Knowledge Check
- Question 1 - Select One
Katie hikes 5 miles north, 7 miles east, and then 3 miles north again. What number of miles, measured in a straight line, is katie from her starting point?
A√83B10C√113D13 - Question 2 - Select One

When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)A7.2B9.5C10.6D15
A person moves towards East for 3 m, then towards North for 4 m and then moves vertically up by 5 m. What is his distance now from the starting point ?
View SolutionAn insect is at the bottom of a hemispherical ditch of radius 1 m. It crawls up the ditch but starts slipping after it is at height h from the bottom . If the coefficient of friction between the ground and the insect is 0.75 , then h is : (g=10ms−2)
View SolutionA spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20cm as shown in the figure. The refractive index of the material of the sphere is equal to √2 and the height of the spider from the centre of the sphere is 2R(=40cm). An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of π/4cm/s. For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
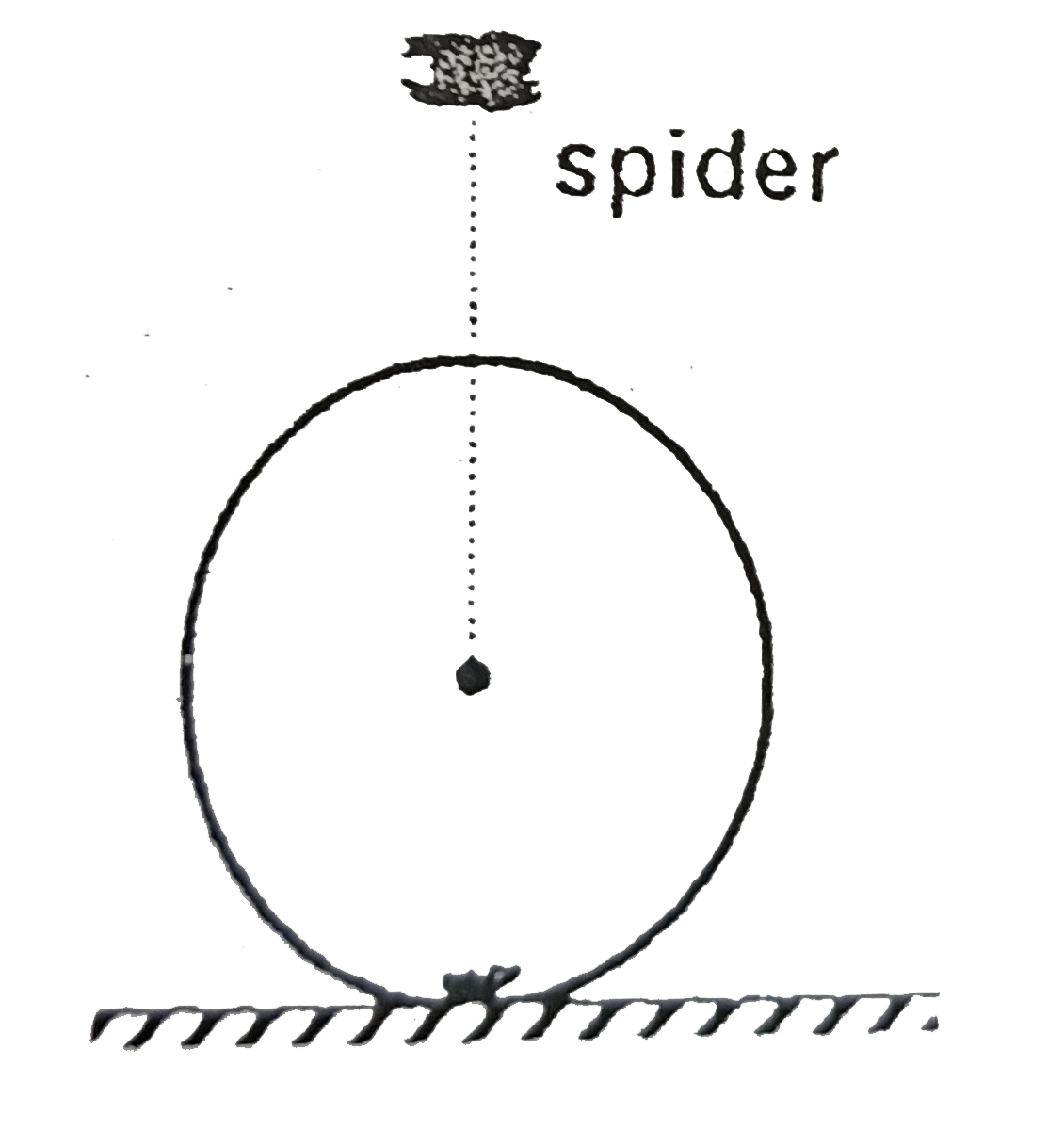 View Solution
View SolutionAn insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
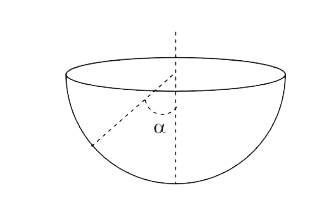 View Solution
View SolutionA heavy block B is sliding with constant velocity u=5m/s on a horizontal table. The width of the block is L=4m.
There is an insect A at distance d=3m from the block as shown in the figure. The insect wants to cross to the oposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v (in m/s) for which the insect can cross to the other side without getting hit by the block.
 View Solution
View Solution
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline thenView Solution

