A block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
The correct Answer is:gtan(α−φ)≤a≤gtan(α+φ), where φ= arctan μ

Since the block does not slide on the wedge, the direction of the force of kinetic friction is not known. Evidently, if the acceleration of the wedge is small, the block will slide downwards and the friction force will be directed as shown in Fig.. When the acceleration of the block is large, the wedge slides upwards and the direction of the block of friction changes sign (see Fig.).
Write down the equations of motion along the coordinate axes for both cases:
y-axis : Qcosα+Tsinα−mg=0,Qcosα−Tsinα−mg=0
x-axis : Qsinα−Tcosapha=ma1,Qsinα+Tcosα=ma2
Noting that T=μQ, we obtain after some transformations:
a1=gtanα−μ1+μtanα,a2=gtanα+μ1−μtanα
Writing μ=tanφ, we obtain gtan(α−φ)≤a≤gtan(α+φ).
Similar Questions
Knowledge Check
If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
 AμgBg(1+μ1−μ)Cg(1−μ1+μ)Dgμ
AμgBg(1+μ1−μ)Cg(1−μ1+μ)Dgμ
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
View SolutionThe coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionA small body A starts sliding down from the top of a wedge (see fig) whose base is equal to l. The coefficient of friction between the body and wedge surface is μ=1.0. At what value of angle q will the time of sliding be least?
View SolutionIn figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
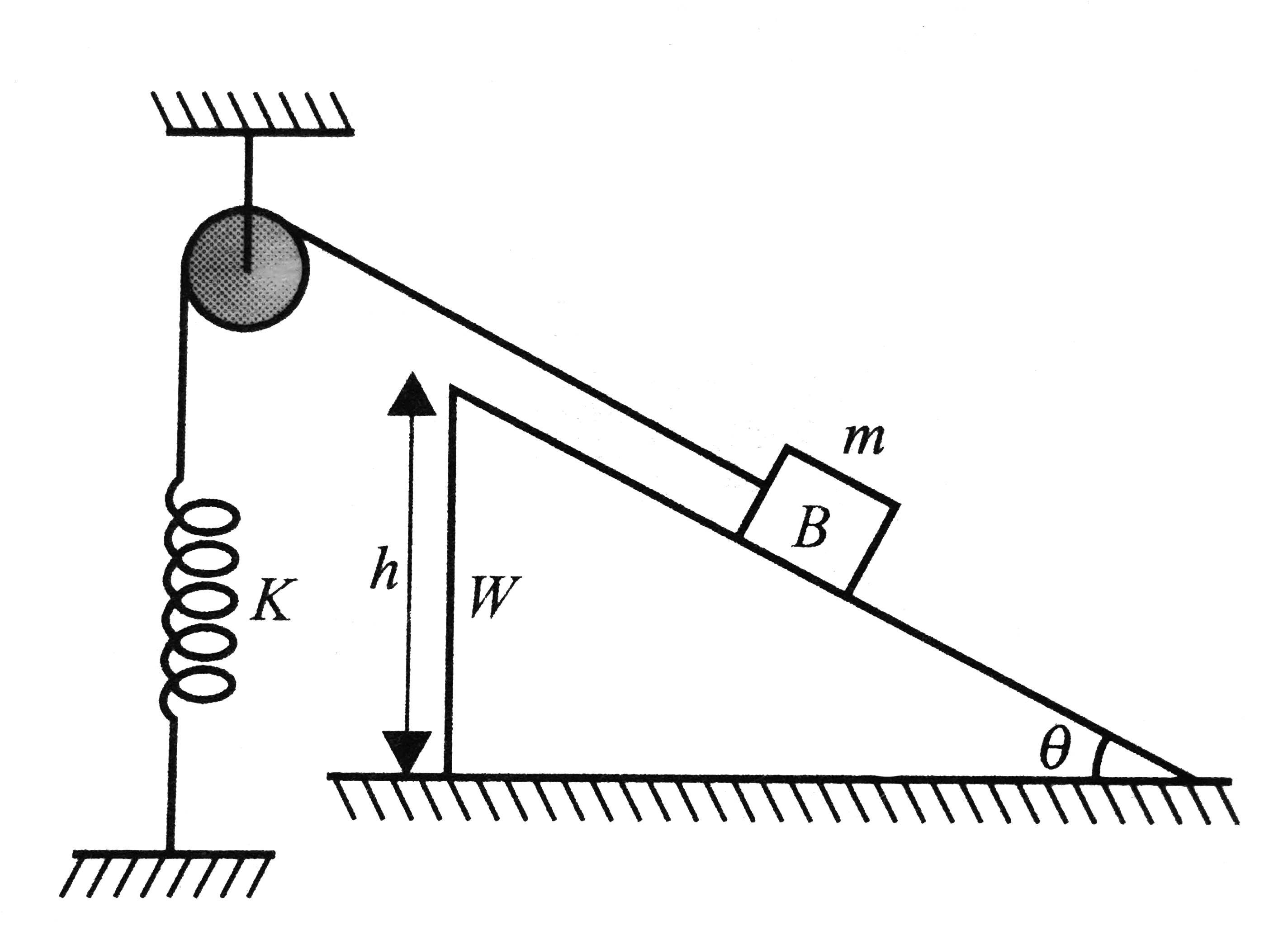
View SolutionIn figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.

View Solution

