A relativistic proton with kinetic energy K collides with a stationary proton. Assuming the collision to he elastic and the energy to be partitioned equally between the particles, find the scattering angle. Calculate for the cases K = = 500 MeV and K = 10 GeV.

Text Solution

Verified by Experts

The correct Answer is: $83^{\circ}; 43^{\circ}$

Since the energy is equipartitiened between the particles, the same will happen lo the momenta. Consequently, after the collisions the protons scatter at equal angles to the original direction of the proton projectile (see Fig. 10.6). From the laws of conservation of total momentum and of total kinetic energy we obtain
$2 p_{1} \frac{cos α}{2} = p, 2 K_{1} = K$
From the relation between the energy and the momentum $E^{2} =$

$= E_{0}^{2} + p^{2} c^{2}$ we obtain, nothing that $E = E_{0} + K$
$K^{2} + 2 K E_{0} = p^{2} c^{2}, K_{1}^{2} + 2 K_{1} E_{0} = p_{1}^{2} c^{2}$
Eliminating the momenta and the proton.s kinetic energy after collision, $K_{1}$ , from these equations, we obtain
$\frac{{cos}^{2} (α)}{2} = \frac{2 E_{0} + K}{4 E_{0} + K}$
whence
$cos α = 2 \frac{{cos}^{2} (α)}{2} - 1 = \frac{K}{4 E_{0} + K}$
Note that in the nonrelativistic case, when $K < < E_{0}$ , we shall have $cos α \approx 0$ and $α \approx \frac{π}{2}$ .
For K = 500 MeV we obtain, noting that $E_{0} = 938 M e V, cos α = 0.117, α = 0.46 π$ .
For K = 10 GeV we obtain $cos α : = 0.728, α := 0.24 π$ . We see that as the kinetic energy of the projectile particle rises, the scattering angle decreases, approaching zero for ultra-relativistic particles $(K > > E_{0})$ .

|

Class 12 PHYSICS CENTRE OF MASS

Similar Questions

Knowledge Check

A proton with kinetic energy $K$ , strikes another proton at rest. If the collision is head-on, find the correct graph between $K$ and the distance of closest approach, $r$ .
A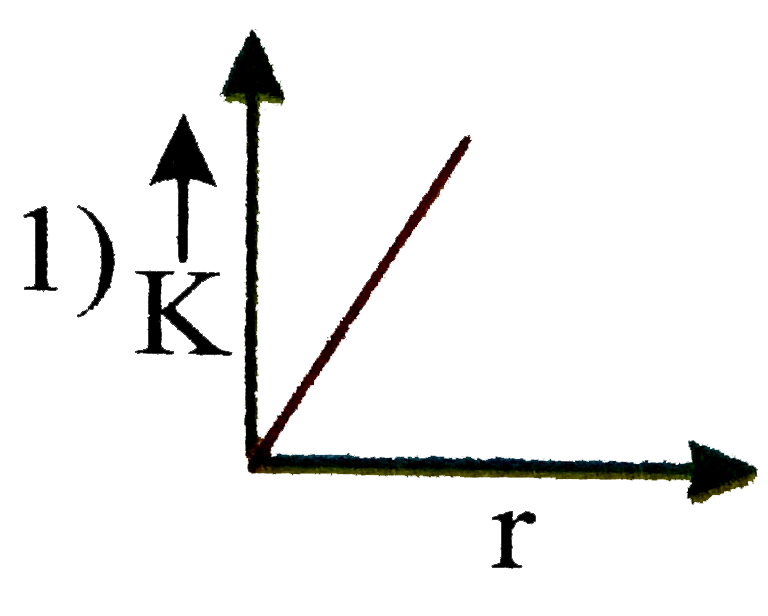
B
C
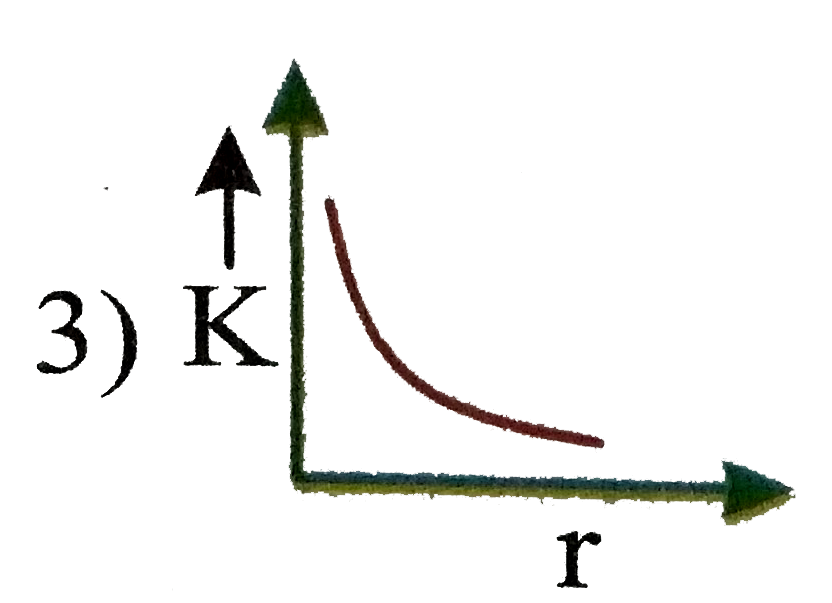D
A particle of mass $m$ moving with kinetic energy $K$ , makes a head - on elastic collision with a stationary particle of mass $η m$ . The maximum potential energy stored in the system during the collision is
A $\frac{η}{η + 1} K$
B $\frac{η + 1}{η} K$
C $(η - 1) K$
D $(η - 1) K$
The relation between kinetic energy K and linear momentum p of a particle is represented by
A $K^{2} = 2 m p$
B $2 K^{2} = m p$
C $p^{2} = 2 m k$
D $2 m K = p$

Recommended Questions

Home
Ask Doubt
Profile