State Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor . Solution in Kannada
Statement : The line integral of magnetic field around any closed path in free space is equal to μ0 times the net current enclosed by that path.
i.e., ∮→B.d→I=μ0I
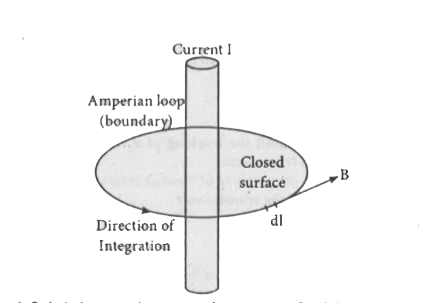
Consider a infinitely long conductor carrying a current . Let Ie be the current enclosed by the loop and L be the length of the loop for which .B. is tangential , then the amperes circuital law ∮→B.d→I=μ0I becomes BL=μ0I
If we assume a straight conductor and the boundary of the surface surrounding the conductor as a circle , then length of the boundary is the circumference , 2πr , where .r. is the radius of the circle . Then B. 2πr=μ0I
∴B=μ0I2πr
Topper's Solved these Questions
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015EXERCISE - PART-D11videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014EXERCISE - PART-D (VI. Answer any three of the following questions.)5videos
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
- BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JUNE-2019EXERCISE - Part-C18videos
SUPPLEMENTARY EXAM QUESTION PAPER JUNE-2019
Similar Questions
Derive an expression for the electric field at a point due to an infinitely long thin charged straight wire using Gauss Law.
02:54View SolutionTwo charges 3x10−8C & −2x10−8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential infinity to be 0.
02:55View SolutionMention and five properties of electric field lines.
05:24View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
03:30View SolutionObtain an expression for the magnetic field at a point due to an infinitely long thin conductor or wire by applying Ampere's circuital law.
05:24View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
03:43View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
05:57View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
05:24View SolutionUsing Ampere.s circuital law derive an expression for magnetic field due to infinitely long current carrying wire at a point at distance Yfrom it.
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
03:25View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
05:57View SolutionState Biot-Savart.s law. Derive an expression for magnetic field at a point near an infinitely long and straight current carrying conductor.
02:51View SolutionState Ampere's circuital law. Derive an expression for magnetic field due to long solenoid .
02:03View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
02:51View SolutionUsing Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
02:51View Solution

