A boy of mass 30 kg is sitting at a distance of 2 m from the middle of a see-saw. Where should a boy of mass 40 kg sit so as to balance the see-saw ?
To solve the problem of balancing the see-saw with two boys of different masses, we can use the principle of moments. The principle states that for a see-saw to be balanced, the clockwise moments must equal the counterclockwise moments about the pivot point (the center of the see-saw).
1. Identify the Masses and Distances:
- Mass of the first boy (m1) = 30 kg
- Distance of the first boy from the center (d1) = 2 m
- Mass of the second boy (m2) = 40 kg
- Distance of the second boy from the center (d2) = ? (This is what we need to find)
2. Write the Moment Equation:
The moment (torque) is calculated as the product of mass and distance from the pivot. For the see-saw to be balanced:
m1×d1=m2×d2
Substituting the known values:
30kg×2m=40kg×d2
3. Calculate the Left Side:
30×2=60kg m
4. Set Up the Equation:
60=40×d2
5. Solve for d2:
To find d2, divide both sides by 40:
d2=6040=1.5m
6. Conclusion:
The boy of mass 40 kg should sit 1.5 meters away from the center of the see-saw to balance it.
Final Answer:
The boy of mass 40 kg should sit 1.5 meters away from the center of the see-saw.
- Mass of the first boy (m1) = 30 kg
- Distance of the first boy from the center (d1) = 2 m
- Mass of the second boy (m2) = 40 kg
- Distance of the second boy from the center (d2) = ? (This is what we need to find)
The moment (torque) is calculated as the product of mass and distance from the pivot. For the see-saw to be balanced:
m1×d1=m2×d2
Substituting the known values:
30kg×2m=40kg×d2
30×2=60kg m
60=40×d2
To find d2, divide both sides by 40:
d2=6040=1.5m
The boy of mass 40 kg should sit 1.5 meters away from the center of the see-saw to balance it.
The boy of mass 40 kg should sit 1.5 meters away from the center of the see-saw.
Topper's Solved these Questions
Similar Questions
On a see saw, two chlidren of masses of 30kg and 50kg are sitting on one side of at distances 2m and 2.5m respectively from its middle. Where should a man of mass 74 kg sit to balance it?
View SolutionThree children are sitting on a see-saw in such a way that is balances. A 20kg and a 30kg boy are on opposite sides at a distance of 2m from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
View Solution
Knowledge Check
Karan of mass 45kg and Geeta of mass 30kg are sitting on a see saw at a distance of 2m and 1.5m respectively from the centre of the see saw in an amusement park as shown in the figure. Is the see saw in rotational equilibrium?
 AYesBNoCdata incompleteDNone of the above
AYesBNoCdata incompleteDNone of the above
(i) Find the acceleration of the centre of mass of two particle approaching towards each other under their own grabitational field.
(ii) A boy of mass 30 kg is standing on a flat boat so that he is 20 meter from the shore. He walks 8 m on the boat towards the shore and then stops. The mass of the boat is 90 kg and friction between the boat and the water surface is negligible. How far is the boy from the shore now ?
View SolutionA uniform seesaw, 5m long, is supported at its centre. A boy weighing 40 kgf sits at a distance of 1 m from the centre of the seesaw.
(i) To which class of lever does it belong ?
(ii) Find where a girl of weight 20 kgf must sit on the seesaw so as the balance the weight of the boy.
View SolutionA boy of mass 30 kg is standing at one end on a stationary boat over a lake. The boat has a mass 70 kg and length 10 m. Now the boy walked to the other end of the boat. Relative to the ground
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
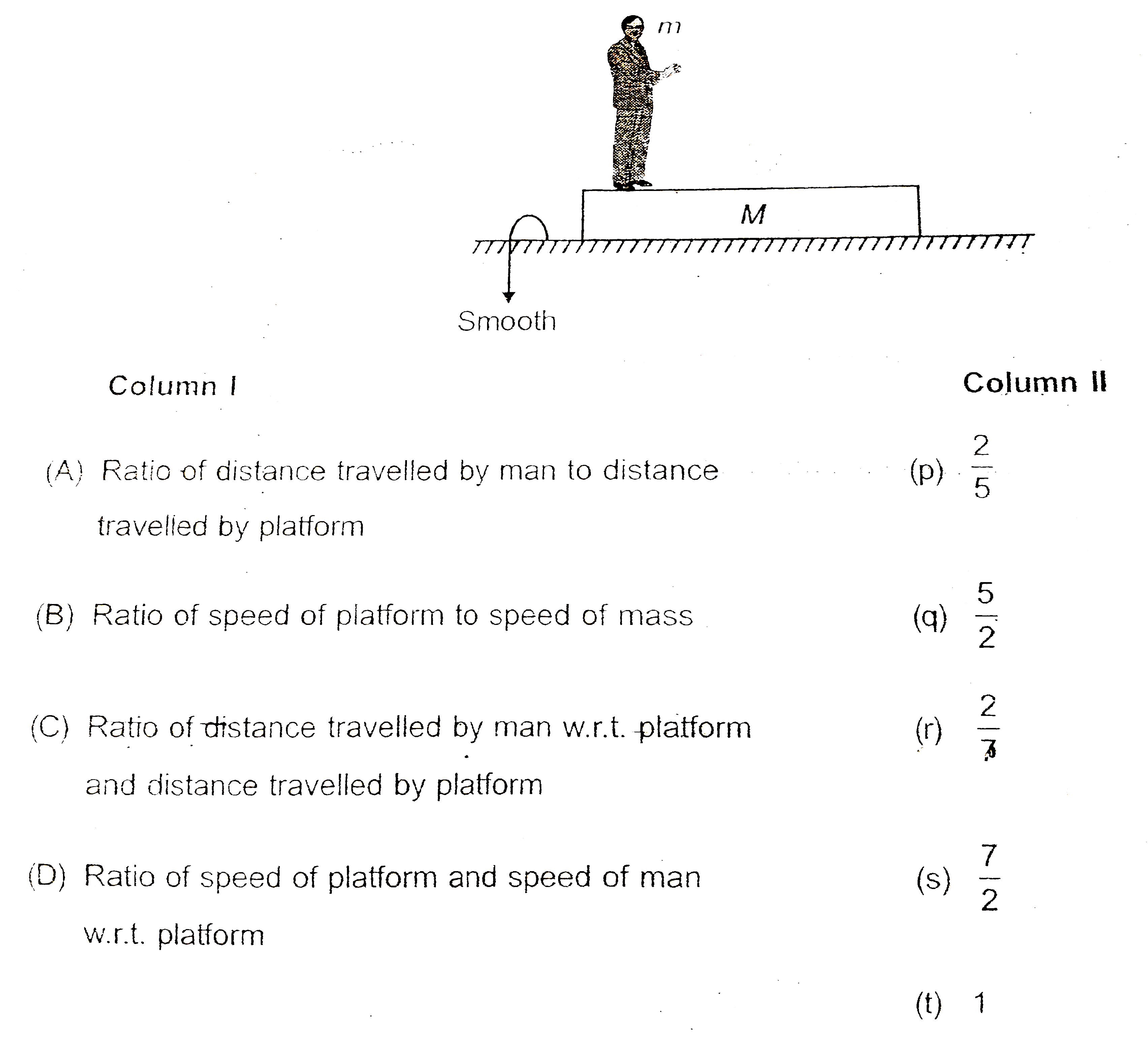
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionIN a typical Indian Bugghi(a luxury cart drawn by horses), a wooden plate is fixed on the rear on which one person can sit. A bugghi of mass 200 kg is moving at a speed of 10 km/h. As it overtakes a school boy walking at a speed of 4 km/h,. the boy sits on the wooden plate. If the mass of the boy is 25 kg, what will be the new velocity of the bugghi?
View SolutionA boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View Solution
