A uniform seesaw, 5m long, is supported at its centre. A boy weighing 40 kgf sits at a distance of 1 m from the centre of the seesaw.
(i) To which class of lever does it belong ?
(ii) Find where a girl of weight 20 kgf must sit on the seesaw so as the balance the weight of the boy.
To solve the problem step by step, we will address both parts of the question.
Step 1: Identify the Class of Lever
A seesaw is a type of lever. In this case, the seesaw is supported at its center, which acts as the fulcrum. The boy sitting on one side creates a load, while the other side will have the girl sitting to balance it.
Answer: The seesaw belongs to Class 1 lever because the fulcrum is located between the load (the boy) and the effort (the girl).
Step 2: Set Up the Equation for Balancing the Seesaw
To find where the girl must sit to balance the seesaw, we can use the principle of moments. The moments on either side of the fulcrum must be equal for the seesaw to be balanced.
The formula for moments is:
Load×Load Arm=Effort×Effort Arm
In this case:
- Load (weight of the boy) = 40 kgf
- Load Arm (distance from the center to the boy) = 1 m
- Effort (weight of the girl) = 20 kgf
- Effort Arm (distance from the center to the girl) = x (unknown)
Step 3: Write the Moment Equation
Substituting the known values into the moment equation, we get:
40kgf×1m=20kgf×x
Step 4: Solve for x
Now, we can solve for x:
40=20x
Dividing both sides by 20:
x=4020=2m
Step 5: Conclusion
The girl must sit 2 meters from the center of the seesaw to balance the weight of the boy.
Final Answers:
(i) The seesaw belongs to Class 1 lever.
(ii) The girl must sit 2 meters from the center of the seesaw.
---
A seesaw is a type of lever. In this case, the seesaw is supported at its center, which acts as the fulcrum. The boy sitting on one side creates a load, while the other side will have the girl sitting to balance it.
To find where the girl must sit to balance the seesaw, we can use the principle of moments. The moments on either side of the fulcrum must be equal for the seesaw to be balanced.
Load×Load Arm=Effort×Effort Arm
- Load (weight of the boy) = 40 kgf
- Load Arm (distance from the center to the boy) = 1 m
- Effort (weight of the girl) = 20 kgf
- Effort Arm (distance from the center to the girl) = x (unknown)
Substituting the known values into the moment equation, we get:
40kgf×1m=20kgf×x
Now, we can solve for x:
40=20x
Dividing both sides by 20:
x=4020=2m
The girl must sit 2 meters from the center of the seesaw to balance the weight of the boy.
(i) The seesaw belongs to Class 1 lever.
(ii) The girl must sit 2 meters from the center of the seesaw.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MACHINESEXERCISE - EXERCISE-3(A)40videos
MACHINES
- BOOK - ICSECHAPTER - MACHINESEXERCISE - EXERCISE-3(A) MULTIPLE CHOICE TYPE5videos
MACHINES
- BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)2videos
HOUSEHOLD CIRCUITS
- BOOK - ICSECHAPTER - QUESTION PAPER 2022 TERM 1EXERCISE - MULTIPLE CHOICE QUESTIONS40videos
QUESTION PAPER 2022 TERM 1
Similar Questions
A boy of mass 30 kg is sitting at a distance of 2 m from the middle of a see-saw. Where should a boy of mass 40 kg sit so as to balance the see-saw ?
View SolutionWhen a boy weighing 20 kgf sits at one end of a 4m long see saw, if gets depressed at this end. How can it be brought to the horizontal position by a man weighing 40 kgf.
View Solution
Knowledge Check
- Question 1 - Select One
Three girls Shivangi, Radhika and Saili sat on one side of see saw at distances of 1m, 1.2m and 1.5m from the fulcrum that is situated at the center of the see saw. The masses of the three girls were 30kg, 40kg and 50kg respectively. Where should Rakesh sit on the other side of seesaw so as to balance it? Given the mass of Rakesh is 80kg.
A2mB1.5mC1.91mD1.75m
In Fig.1.35 a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium find the reaction R1andR2 at the ends.
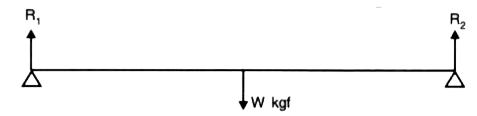 View Solution
View SolutionA fire tongs has its arms 20 cm long. It is used to lift a coal of weight 1.5 kgf by applying an effort at a distance of 15 cm from the fulcrum. Find : (i) the mechanical advantage of the togns, and (ii) the effort needed.
View SolutionFigure shows a convex lens of focal length 10cm lying in a uniform magnetic field B of magnitude 1.2T parallel to its principal axis.A particle havig a charge 2.0×10−3C and mass 2.0×10−5kg is projected perpendicular to the plane of the diagram with a speed of 4.8m/s.The particle moves along a circle with its centre on the principal axis at a distance of 15cm from the lens.The axis of the lens and of the circle are same.Show that the image of the particle goes along a circle and find the radius of that circle.
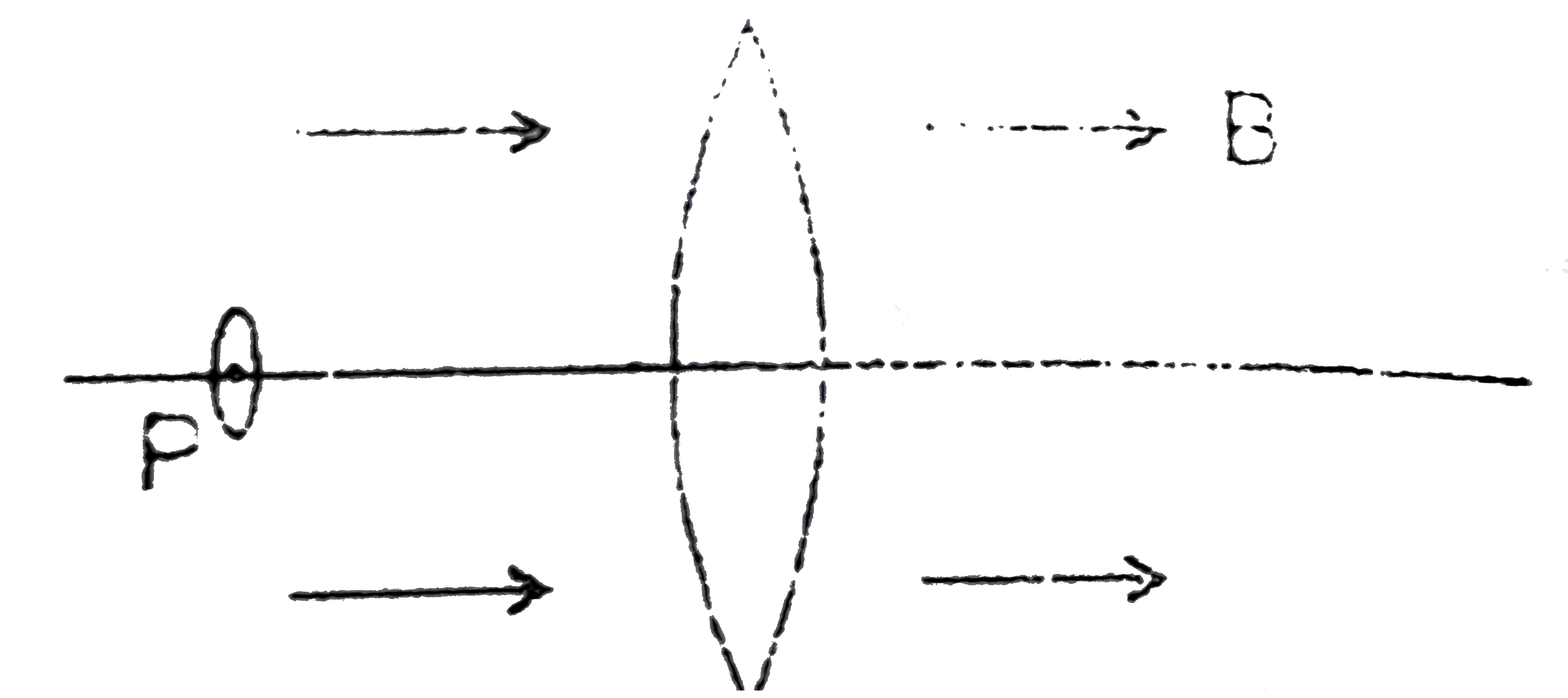 View Solution
View SolutionA 4 m long rod of negligible weight is supported at a point 125 cm from its one end and a load of 18 kgf is suspened at a point 60 cm from the support on the shorter arm.
(a) If a weight W is placed at a distance 250 cm from the support on the longer arm to balance the rod, find W.
(b) If a weight 5 kgf is kept to balance the rod, find its position.
(c) To which class of lever does it belong ?
View SolutionThree children are sitting on a see-saw in such a way that is balances. A 20kg and a 30kg boy are on opposite sides at a distance of 2m from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
View SolutionA long non-conducting, massless rod of length L pivoted at its centre and balanced with a weight w at a distance x from the lefrt end. At the left and right ends fo the rod are attached small conducting sphers with positive charfges q and 2q respectively. A distance h directly beneath each of these spheres is a fixed sphere with positive charge Q.
(a) Find the distance x where the rod is horizontal and balanced.b. What valueshold h have so that the rod exerts no vertical force on the bearing when the rod is horizontal and balanced?View SolutionAnswer the following:
(a) What is a wave front? How does it propagate? Using Huygens' principle, explain reflection of a plane wavefront from a surface and verify the laws of reflection.
(b) A parallel beam of light of wavelength 500nm falls on a narrow slit and the resulting diffraction pattern is obtained on a screen 1m away. If the first minimum is formed at a distance of 2.5mm from the centre of screen, find the
(i) width of the slit, and
(ii) distance of first secondary maximum from the centre of the screen.View Solution

