A neutral spherical copper particle has a radius of 10 nm (1nm=10−9m). It gets charged by applying the voltages slowly adding one electron at a time. Then the graph of the total charge on the particle vs the applied voltage would look like:
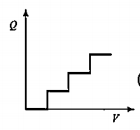
To solve the problem, we need to analyze how the charge on a neutral spherical copper particle changes as we add electrons one by one, and how this affects the voltage (or potential) across the particle.
1. Understanding the Initial Condition:
- The particle is initially neutral, meaning it has no net charge. The radius of the particle is given as 10 nm.
2. Adding Electrons:
- When we add the first electron, the particle gains a negative charge of -1e (where e is the elementary charge, approximately 1.6×10−19C).
- The potential V of a charged spherical conductor is given by the formula:
V=kQR
where k=14πϵ0, Q is the charge, and R is the radius of the sphere.
3. Calculating the Potential for Each Electron Added:
- After adding the first electron, the charge Q=−1e. The potential becomes:
V1=k(−1e)R
- Adding a second electron gives a charge of Q=−2e:
V2=k(−2e)R
- This process continues as we add more electrons.
4. Observing the Pattern:
- Each time we add an electron, the charge increases by −e, and the potential changes linearly with the charge.
- However, since we are adding electrons one at a time, the potential does not change continuously but rather in discrete steps.
5. Graphing Charge vs. Applied Voltage:
- The graph of total charge on the particle (y-axis) versus the applied voltage (x-axis) will resemble a staircase pattern. Each step corresponds to the addition of one electron, resulting in a jump in the charge and a corresponding change in potential.
- Thus, the graph will show horizontal segments (constant potential) followed by vertical jumps (increase in charge).
Conclusion:
The graph of total charge on the particle versus the applied voltage will look like a staircase, indicating that the potential remains constant for each added electron until the next electron is added.
- The particle is initially neutral, meaning it has no net charge. The radius of the particle is given as 10 nm.
- When we add the first electron, the particle gains a negative charge of -1e (where e is the elementary charge, approximately 1.6×10−19C).
- The potential V of a charged spherical conductor is given by the formula:
V=kQR
where k=14πϵ0, Q is the charge, and R is the radius of the sphere.
- After adding the first electron, the charge Q=−1e. The potential becomes:
V1=k(−1e)R
- Adding a second electron gives a charge of Q=−2e:
V2=k(−2e)R
- This process continues as we add more electrons.
- Each time we add an electron, the charge increases by −e, and the potential changes linearly with the charge.
- However, since we are adding electrons one at a time, the potential does not change continuously but rather in discrete steps.
- The graph of total charge on the particle (y-axis) versus the applied voltage (x-axis) will resemble a staircase pattern. Each step corresponds to the addition of one electron, resulting in a jump in the charge and a corresponding change in potential.
- Thus, the graph will show horizontal segments (constant potential) followed by vertical jumps (increase in charge).
The graph of total charge on the particle versus the applied voltage will look like a staircase, indicating that the potential remains constant for each added electron until the next electron is added.
Topper's Solved these Questions
Similar Questions
A spherical oil drop, radius 10−4 cm has on it at a certain a total charge of 40 electrons. Calculate the energy that would be required to place an additional electron on the drop.
View SolutionA particle moves in a circle of radius 1.0cm under the action of a magnetic field of 0.40T.An electric field of 200V/m makes the path straight.Find the charge/mass ratio of the particle.
View Solution
Knowledge Check
- Question 1 - Select One
If 109 electrons move out of a body to another body every second, then the time required to get a total charge of 1 C on the other body is
A250 yearsB100 yearsC198 yearsD150 years - Question 2 - Select One
A point charge produces an electric flux of −1×103Nm2/C to pass through a spherical gaussian surface of radius 10 cm cenred on the charge. What is the value of the point charge?
A7.85×10−6CB8.85×109CC−8.85×10−9CD4.425×10−9C - Question 3 - Select One
If 1018 electrons are taken out every second from a body, then how much time is required to get a total charge of 0.1 C from it?
A0.625sB6.25sC62.5sD625s
Two spherical objects are separated by a distance of 1.80×10−3m. The objects are initially electrically neutral and are very small compared to the distance between them. Each object acquires the same negative charge due to the addition of electrons. As a result, each object experiences an electrostatic force that has a magnitude of 4.55×10−21N. How many electrons did it take to produce the charge on one of the objects ?
View SolutionA thin fixed of radius 1 metre has a positive charge 1×10−5 coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of 1×10−6 coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
View SolutionIf a body gives out 109 electrons every second, how much time required to get a total charge of 1C from it ?
View SolutionA particle having a charge of 1.6x10−19C enters midway between the two plates of a parallel plate capacitor. The initial velocity of particle is parallel to the plates. A potential difference of300 Vis applied between the two plates. lfthe length of the plates is 10 cm and they are separated by 2 cm, calculate the greatest initial velocity for which the particle will not be able to come out of the plates. The mass of the particle is 12×10−24kg
[104m/s]View SolutionOne particle has a mass of 3.0×10−3kg and a charge of +8.00μC. A second particle has a mass of 6.0×10−3 kg and place and then released. The particles fly apart, and when the separation between them is 0.100 m, the speed of the 3.00×10−3 kg particle is 125 mis. Find the initial separation between the particles.
View Solution

